Решение. Подынтегральная функция на отрезке a = 0 и b = 1 равна .
Подынтегральная функция на отрезке a = 0 и b = 1 равна Находим шаг вычислений
Отсюда точки иртегрирования:
Тогда по формуле трапеций имеем
Ответ: Пример 16.2. Пользуясь формулой трапеций вычислить определённый интеграл
Пример 16.3. Пользуясь формулой трапеций вычислить определённый интеграл
[kgl].
[gl] Тема 17. Метод Симпсона (парабол). Геометрическая инртерпретация метода [:]
Если заменить график функции y = f (x) на каждом отрезке [ x I – 1; xi ] разбиения не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближённого вычисления интеграла Предварительно найдём площадь S криволинейной трапеции, ограниченной сверху графиком параболы y = ax 2 + bx + c (с осью симметрии, параллельной оси ординат Oy), сбоку – прямыми x = – h, x = h и снизу – отрезком [– h; h ]. Пусть парабола проходит через три точки

Рисунок 17.1 – К элементарной формуле парабол Площадь S равна
Выразим эту площадь через h, y 0, y 1, y 2. Из равенств для ординат yi находим, что
Получим теперь формулу парабол для приближённого вычисления интеграла Для этого отрезок [ a; b ] разобьём на 2 n частей (отрезков) длиной В точках деления
Рисунок 17.2 – Приближённое вычисление интеграла по формуле Симпсона (парабол) Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями, равными h, одной элементарной параболической трапецией с основанием, равным 2 n. На отрезке [ x 0, x 2] парабола проходит через три точки (x 0; y 0), (x 1; y 1); (x 2; y 2). Используя формулу (17.2), находим
Аналогично находим
Сложив полученные равенства, имеем
или
Формула (17.3) называется формулой парабол (или Симпсона).
Пример 17.1. Вычислить приближённо определённый интеграл
|

 .
.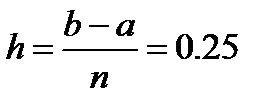 .
.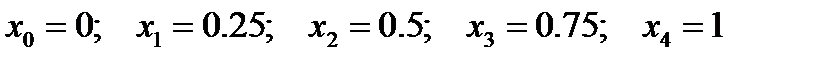 .
. .
. .
. .
. .
. .
. , где
, где 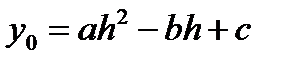 – ордината параболы в точке x = – h; y 1 = c – ордината параболы в точке x = 0;
– ордината параболы в точке x = – h; y 1 = c – ордината параболы в точке x = 0;  – ордината параболы в точке x = h (рисунок 17.1).
– ордината параболы в точке x = h (рисунок 17.1). . (17.1)
. (17.1) . Подставляя эти значения c и a в равенство (17.1), получаем
. Подставляя эти значения c и a в равенство (17.1), получаем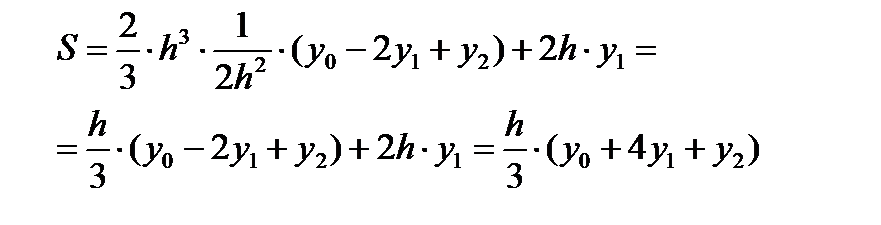 . (17.2)
. (17.2)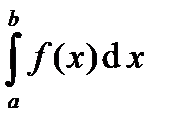 .
.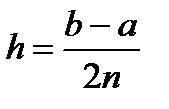 точками
точками 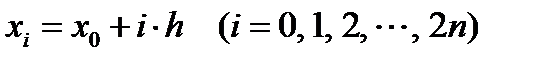 .
. вычисляем значения подынтегральной функции f (x):
вычисляем значения подынтегральной функции f (x):  , где yi = f (xi) (рисунок 17.2).
, где yi = f (xi) (рисунок 17.2).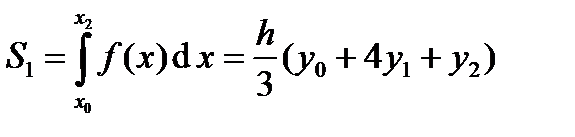 .
.


 (17.3)
(17.3) , разбив отрезок [0; 2] на 4 части.
, разбив отрезок [0; 2] на 4 части.


