Свойства детерминантов
Рассмотрим свойства детерминантов на примере детерминанта 3-го порядка. Свойство 1. Детерминант не изменится, если его строки заменить столбцами, и наоборот.
Свойство 2. При перестановке двух параллельных рядов детерминант меняет знак. Свойство 3. Детерминант, имеющий два одинаковых ряда, равен нулю. Свойство 4. Общий множитель элементов какого-либо ряда детерминанта можно вынести за знак детерминанта. Свойство 5. Если элементы какого-либо ряда детерминанта представляют собой суммы двух слагаемых, то детерминант может быть разложен на сумму двух соответствующих детерминантов. Например,
Свойство 6. Детерминант не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число. Минором некоторого элемента aij детерминанта n -го порядка называется детерминант порядка, полученный из исходного путём вычёркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначим mij. Так, если
Алгебраическим дополнением элемента aij детерминанта называется его минор, взятый со знаком «+», если сумма i + j – чётное число, и со знаком «–», если эта сумма нечётная. Обозначается Aij = (–1) i + j · mij. Так, A 11 = + m 11, A 32 = – m 32. Свойство 7. («Разложение детерминанта по элементам некоторого ряда»). Детерминант равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения. Например
Свойство 7 содержит в себе способ вычисления детерминантов высоких порядков. Свойство 8. Сумма произведений элементов какого-либо ряда детерминанта на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. Так, например, a 11· A 21 + a 12· A 22 + a 13· A 23 = 0.
[kgl].
[gl] Тема 11. Понятие невырожденной матрицы. Обратная матрица. Этапы нахождения обратной матрицы [:]
Пусть A – квадратная матрица n -го порядка
Квадратная матрица A называется невырожденной, если детерминант Δ = det A не равен нулю: Δ = det A ≠ 0. В противном случае (Δ = 0) матрица A называется вырожденной. Матрица A –1 называется обратной матрице A, если выполняется условие A · A –1 = A –1 · A = E, где E – единичная матрица того же порядка, что и матрица A. Матрица A –1 имеет те же размеры, что и матрица A. Теорема. Всякая невырожденная матрица имеет единственную матрицу A –1 = B, элементы которой находятся по формуле
Из теоремы вытекает правило: чтобы найти обратную матрицу к матрице (11.1), надо пройти следующие этапы преобразования: 1. Вычислить детерминант Δ матрицы A (Δ = det A ≠ 0). 2. Каждый элемент матрицы A заменить его алгебраическим дополнением, т. е. составить матрицу (Aij). 3. Транспонировать матрицу (Aij), т. е. записать матрицу (Aji). 4. Матрицу (Aji) умножить на В результате получим матрицу A –1. Пример 11.1. Найти матрицу A –1, обратную к матрице
Решение: 1. Вычисляем детерминант данной матрицы
Т. к. det A = 5 ≠ 0, то матрица A имеет обратную матрицу A –1. 2. Находим алгебраические дополнения
Составляем матрицу (Aij) из алгебраических дополнений
3. Транспонируем полученную матрицу, т. е. переходим к матрице (Aji)
4.Умножая на
|

 .
.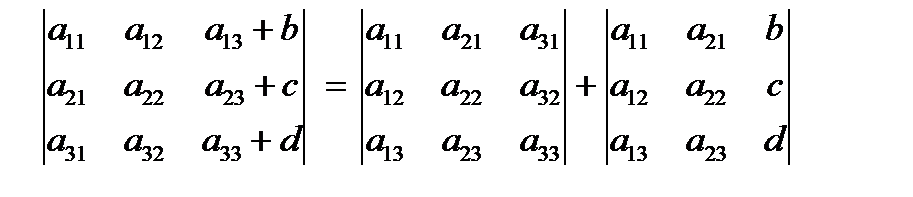 .
. , то
, то  ,
,  .
.
 . (11.1)
. (11.1) .
. .
.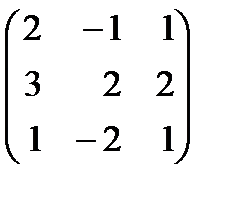 .
.
 .
.



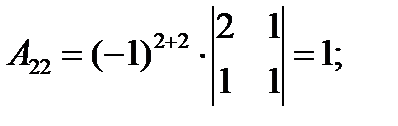
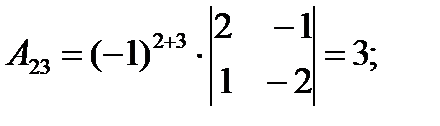



 .
. .
. , получим обратную матрицу
, получим обратную матрицу . (11.2)
. (11.2)


