Решение. Для отделения корней исследовалась производная уравнения F ′(x) = 15 x2 – 20, корни которой легко определились аналитически: это ±2/
Для отделения корней исследовалась производная уравнения F ′(x) = 15 x 2 – 20, корни которой легко определились аналитически: это ±2/
Следовательно, корни расположены на отрезках [–3; –2]; [0; 1] и [1; 2]. Теперь уравнение F(х) = 0 следует привести к виду x = ψ (x), что можно сделать разными способами, например: 1) 2) 3) Определим, какой из полученных функций ψ(x) следует воспользоваться для вычисления последовательных приближений. Итерационный процесс сходится, если | ψ`(x)| < 1. Выберем на отрезке [0; 1] произвольную точку x 0. Пусть x 0 = 0.5. Тогда
Проверим условие сходимости итерационного процесса:
Следовательно, для вычисления последовательных приближений можно использовать только ψ3(x). Тогда, выбирая x 0 = 0.5, определим x 1 = ψ (x 0), т. е.
Если | x 2 – x 1| ≤ ε, то x 1 – корень уравнения. В противном случае вычисляем x 2 = ψ (x 1), т. е.
Затем снова следует проверка | x 2 – x 1| ≤ ε Если условие выполняется, то x 2 – корень уравнения, в противном случае вычисляется величина x 3 = ψ (x 2). Процесс продолжается до тех пор, пока не будет достигнута требуемая точность.
Пример 6.2. Методом итераций уточнить с точностью до 10 –4 корень уравнения
|
. Определим знаки функции на интервалах
.
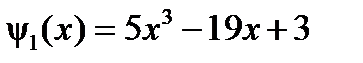, тогда 
;
, тогда 
;
, тогда 
.
– расходящийся итерационный процесс;
– сходящийся итерационный процесс.
.
.
.
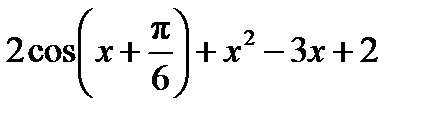