Решение. Первоначально корни уравнения определяем с точностью ε = 0.1 графическим методом, а затем найденное значение корня уточняем до 0.0001.
Первоначально корни уравнения определяем с точностью ε = 0.1 графическим методом, а затем найденное значение корня уточняем до 0.0001. Перепишем уравнение в виде
Если построить два графика:
[kgl].
[gl] Тема 7. Метод линейной интерполяции (метод хорд) в решении уравнений. Геометрическая интерпретация метода [:]
Если x 0, x 1 – приближённые значения корня уравнения f (x) = 0, a f (x 1) · f (x 2) < 0, то последующие приближения находят по формуле
Методом хорд называют также метод, при котором один из концов отрезка [a; b] закреплён (рис. 7.1), т. е. вычисление приближения корня уравнения f (x) = 0 производят по формулам
При расчёте предполагается, что корень уравнения находится на отрезке [а; b], a f "(x) сохраняет знак на [а; b]. Из рисунка 7.1 видно, что получаемые точки xc постепенно сходятся к корню уравнения. Поскольку в рассмотренном методе очередное приближение xc определяется с помощью интерполяции, учитывающей наклон кривой f (x), он во многих случаях оказывается более эффективным, чем метод половинного деления.
Рисунок 7.1 – Метод хорд Пример 7.1. Методом хорд найти корень уравнения Решение Положительный корень будет находиться на отрезке [1; 1.7], так как
Найдём первое приближённое значение корня по формуле
Так как f (1.588) = –0.817 < 0, то применяя вторично способ хорд к отрезку [1.588; 1.7], найдём второе приближённое значение корня:
Теперь найдём третье приближённое значение:
После этого найдём четвёртое приближённое значение:
Следовательно, искомый корень с точностью до 0.01 равен 1.64. Комбинированный метод секущих – хорд Этот метод обеспечивает гарантированную сходимость при выборе в пределах отрезка [ a, b ] двух приближений: нулевого x 0 и первого x 1. Он реализуется алгоритмом, описываемым для метода Ньютона с заменой производной F ′(x) её приближённым значением – множитель перед F (xn):
На рисунке 7.2 показана схема алгоритма комбинированного метода секущих – хорд.
Рисунок 7.2 – Схема алгоритма метода секущих – хорд [kgl]. [gl] Тема 8. Метод Ньютона (касательных). Модификация метода Ньютона. Метод секущих. Схемы метода Ньютона и метода секущих. Схема алгоритма [:]
Если х 0 – начальное приближение корня уравнения f (x) = 0, то последовательные приближения находят по формуле
Если f ′ и f ″ (первая и вторая производные) непрерывны и сохраняют определённые знаки на отрезке [ a; b], а f (a) · f (b) < 0, то, исходя из начального приближения На практике часто используют модификации метода Ньютона, свободные от этого недостатка. Одно из упрощений сводится к тому, что производная вычисляется только один раз в начальной точке и затем это значение используется на всех последующих шагах. Данная модификация основывается на предположении о малом изменении производной вблизи корня. Одной из наиболее известных модификаций является метод секущих. В этом методе производная заменяется её приближённым значением:
В формуле для F'(x) в отличие от f ′(x) приращение
Рисунок 8.1 – Метод Ньютона (a) и метод секущих (b) Выберем на отрезке [ a; b] произвольную точку x 0 – нулевое приближение. Затем найдём
далее
Таким образом, процесс нахождения корня уравнения сводится к вычислению чисел xn по формуле
Процесс вычисления продолжается до тех пор, пока не будет выполнено условие
Схема итерационного процесса метода Ньютона приведена на рисунке 8.2, из которого понятно, что каждое следующее приближение может быть определено по формуле
Рисунок 8.2 – Схема алгоритма метода Ньютона Пример 8.1. Методом Ньютона (касательных) найти корень уравнения Решение В этом уравнении f (x) = Так как f (x) и f "(x) при x0 = 1.7 имеют один и тот же знак, а именно f (1.7) = 0.952 > 0 и f "(1.7) > 0, то применяем формулу
где f ′(1.7) = 4 1.73 – 2 = 17.652. Тогда
Применяем второй раз способ касательных:
где f (x 1) = f (1.646) = 0.048, f ′(1.646) = 15.838;
Следовательно, искомый корень с точностью до 0.01 равен 1.64. Пример 8.2. Методом Ньютона (касательных) найти действительный корень уравнения Решение Записав данное уравнение в виде x 3 = –х + 3 и построив графики функций f 1 (x) = x 3 и f 2 (x) = – х + 3, найдем, что единственный корень уравнения принадлежит отрезку [1; 2]. Определим отрезок меньшей длины, на котором находится корень. Так как f (1.3) = (1.3)3 + 1.3 – 3 = 0.497 > 0, то корень лежит на отрезке [1.2; 1.3]. Серединой этого отрезка является точка x = 1.25. Поскольку f (1.25) = (1.25)3 + 1.25 – 3 = 0.203125 > 0 и f (1.2) < 0, то искомый корень принадлежит отрезку [1.20; 1.25]. Данная функция Результаты вычислений записываем в таблице 8.1, из которой видно, что искомый корень x = 1.21341. Таблица 8.1 – Метод касательных
[kgl].
[gl] Тема 9. Матрицы. Квадратная и транспонированная матрица. Действия над матрицами [:]
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде
или, сокращённо, A = (aij), где Матрицу A называют матрицей размера m × n и пишут Am × n. Числа aij, составляющие матрицу, называются её элементами. Элементы, стоящие на диагонали, идущей из левого верхнего угла, образуют главную диагональ. Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е. A = B, если aij = bij, где Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера n × n называют матрицей n -го порядка. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой E. Пример 9.1.
– единичная матрица 3-го порядка
– единичная матрица n -го порядка. Квадратная матрица называется треугольной, если все её элементы, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нулевой. Обозначается латинской буквой O. Имеет вид
В матричном исчислении матрицы O и E играют роль чисел 0 и 1 в арифметике. Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид
Матрица размера 1 × 1, отождествляется с этим числом, т. е. (5)1×1 есть 5. Матрица, полученная из данной заменой каждой её строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается AT. Так, если Транспонированная матрица обладает следующим свойством: (AT) T = A.
|

 .
. и
и  , то можно убедиться, что один корень равен ≈1.1, а второй – ≈2.9. Поэтому первый интервал выбираем [0.9; 1.3], второй – [2.7; 3.1].
, то можно убедиться, что один корень равен ≈1.1, а второй – ≈2.9. Поэтому первый интервал выбираем [0.9; 1.3], второй – [2.7; 3.1].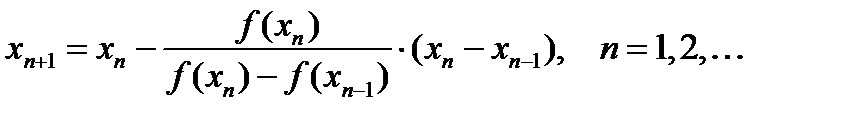 .
.
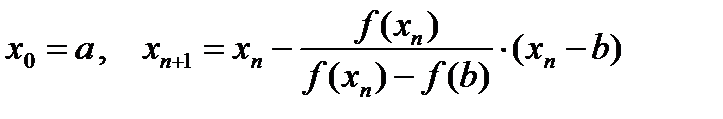 .
.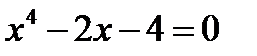 с точностью до 0.01.
с точностью до 0.01. , а
, а  .
.
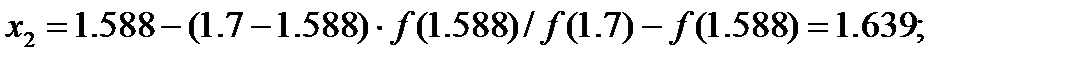
 .
. ;
; .
. ;
;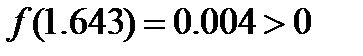 .
. .
. .
. , удовлетворяющего условию f (x0)·f "(x0) < 0, можно вычислить с любой точностью единственный корень уравнения f (x) = 0.
, удовлетворяющего условию f (x0)·f "(x0) < 0, можно вычислить с любой точностью единственный корень уравнения f (x) = 0. .
. , полагается малым, но Δ x ≠ 0. Геометрически это означает, что приближённым значением корня считается точка пересечения секущей, проходящей через две точки функции f (xi) и f (xi + h), с осью абсцисс. Схема метода Ньютона показана на рисунке 8.1 a.
, полагается малым, но Δ x ≠ 0. Геометрически это означает, что приближённым значением корня считается точка пересечения секущей, проходящей через две точки функции f (xi) и f (xi + h), с осью абсцисс. Схема метода Ньютона показана на рисунке 8.1 a. ,
, .
. .
. .
. .
. , f '(x) =
, f '(x) =  , а f "(x) = 12 x 2.
, а f "(x) = 12 x 2. ,
, .
. ,
, ;
;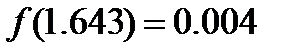 ;
;  ;
;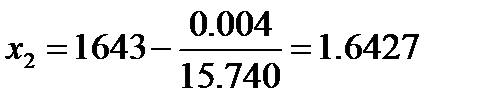 .
. .
. , f (1.2) = (1.2)3 + 1.2 – 3 = –0.072 < 0,
, f (1.2) = (1.2)3 + 1.2 – 3 = –0.072 < 0,
 (т. е. i = 1, 2, 3, …, m) – номер строки,
(т. е. i = 1, 2, 3, …, m) – номер строки,  (т. е. j = 1, 2, 3, …, n) – номер столбца.
(т. е. j = 1, 2, 3, …, n) – номер столбца. .
.

 .
.
 , то
, то  , если
, если  , то
, то  .
.


