Разделим отрезок [ a; b ] на n равных частей, т. е. на n элементарных отрезков. Длина каждого элементарного отрезка  . Точками деления будут:
. Точками деления будут:
 .
.
Эти числа будем называть узлами. Вычислим значения функции f (х) в узлах, обозначим их y 0, y 1, y 2, …, yn. Стало быть,

Числа y 0, y 1, y 2, …, yn являются ординатами точек графика функции, соответствующих абсциссам x 0, x 1, x 2, …, xn (рисунок 15.1).
Рисунок 15.2 – Методы левых (a), правых (b) и средних (c) прямоугольников
Из рисунка 15.2 видно, что площадь криволинейной трапеции приближённо заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определённого интеграла сводится к нахождению суммы n элементарных прямоугольников
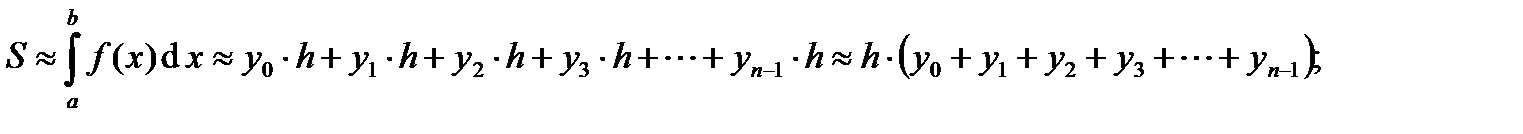 (15.2)
(15.2)
 (15.3)
(15.3)
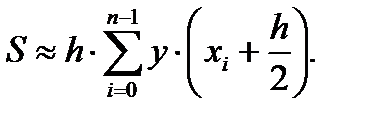 (15.4)
(15.4)
Формула (15.2) называется формулой левых прямоугольников, (15.3) – правых прямоугольников, (15.4) – формулой средних прямоугольников (15.2).
Алгоритм вычисления интеграла по формуле левых прямоугольников показан на рисунке (15.3).
Рисунок 15.3 – Схема алгоритма вычисления интеграла
Пример 15.1. С помощью метода левых и правых прямоугольников вычислить определённый интеграл
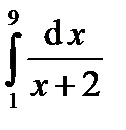 , полагая n = 4.
, полагая n = 4.

 . Точками деления будут:
. Точками деления будут: .
.
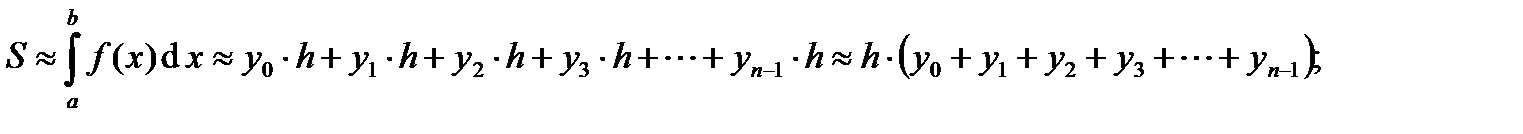 (15.2)
(15.2) (15.3)
(15.3)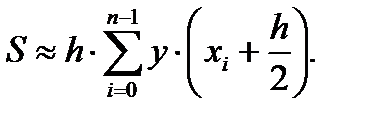 (15.4)
(15.4)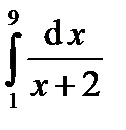 , полагая n = 4.
, полагая n = 4.


