Решение. Эта задача двумерная. Решаем поэтапно:
Эта задача двумерная. Решаем поэтапно:
Рисунок 26.2 – Построение тривиальных ограничений
Рисунок 26.3 – Построение выпуклого многоугольника (ОДР)
Рисунок 26.4 – Построение линий уровня и поиск максимума
[kgl].
[gl] Тема 27. Симплексный метод решения задачи ЛП. Построение опорных планов [:]
Поскольку целевая функция достигает наибольшего значения в крайней угловой точке множества, определяемого системой равенств и неравенств, то нужно проверить все крайние точки этого множества и найти среди них ту, в которой функция F принимает наибольшее значение. Такой метод вполне приемлем для задач с малым числом переменных и ограничений. Однако число крайних точек очень быстро растёт с увеличением числа переменных (n) и ограничений (m) и проведение их сплошной проверки для многих практических задач оказывается очень трудоёмкой. Перебор крайних точек можно упорядочить, если при переходе от одной крайней точки к другой обеспечить возрастание функции цели F. Такое упорядочение достигается применением симплексного метода решения задачи линейного программирования. Среди множества предложенных алгоритмов, этот метод является наиболее эффективным. Этот алгоритм называется ещё методом последовательного улучшения плана. Впервые симплексный метод был предложен американским учёным Дж. Данцигом (J. Dantzig) в 1949 году. Симплексный метод – это итеративный процесс направленного решения системы уравнений по шагам, который начинается с опорного решения и в поисках лучшего варианта движется по угловым точкам области допустимого решения (ODP), улучшающим значение целевой функции до тех пор, пока целевая функция не достигнет оптимального значения. Допустимое множество базисных решений системы линейных уравнений образует в объёме многогранное тело, например, тетраэдр, вершины которого – угловые точки. Каждой угловой точке многогранника решений соответствует опорный план (допустимое базисное решение). Количество перебираемых допустимых базисных решений можно сократить и проводить не беспорядочный перебор, а последовательный по специальному алгоритму, улучшая значение целевой функции. Итеративный переход от одного допустимого базисного решения проводится направленно от одной вершины ODP к другой, заключается в обмене (замещении) базисных и свободных переменных: базисная переменная приравнивается к нулю и переходит в свободную, а соответственно свободная переводится на место базисной. Если в столбце свободных членов все элементы положительны, то решение является допустимым. Если в строке целевой функции все элементы неотрицательные, то решение является оптимальным при решении задачи на максимум. В соответствии с симплексным методом на первом шаге находят начальное опорное решение – допустимый вариант, удовлетворяющий всем ограничениям. Затем последовательно за определённое число итераций направленно осуществляется переход от одного опорного решения к другому вплоть до оптимального. Следует заметить, что на первом шаге в качестве базисных переменных следует выбрать такие m переменные, каждая из которых входит только один раз в одно из m уравнений системы, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных. При этом если выбранные переменные имеют те же знаки, что и соответствующие им свободные члены в правых частях, то полученное базисное решение будет допустимым. В процессе решения системы линейных уравнений необходимо ориентироваться на сохранение неотрицательности всех переменных, поскольку это определяет допустимость решения. Предложенный алгоритм приводит к оптимальному решению для любой модели линейного программирования за конечное число итераций, если система линейных уравнений задачи совместна. Симплексный метод основан на последовательном переходе от одного базисного решения (опорного плана) задачи к другому опорному плану, при этом значение целевой функции изменяется в лучшую сторону. Рассмотрим алгоритм симплексного метода на примере решения задачи об определении оптимального ассортимента продукции.
Таблица
Предприятие может производить два вида изделий A и B, располагая для их изготовления ограниченными ресурсами материала чугуна и стали соответственно в количествах 350 и 394 кг и оборудования в количестве 408 станко-часов. Данные, представленные в виде таблицы, характеризуют затраты каждого из перечисленных трёх видов ресурсов на изготовление одного изделия A и B. Требуется определить, сколько изделий A и B должно производить предприятие, чтобы достичь наибольшей прибыли. Введём искомые неизвестные x 1 и x 2, обозначающие число изделий A и B, которые должно производить предприятие. Тогда математическую задачу можно сформулировать следующим образом. Среди множества неотрицательных решений системы неравенств
найти такое решение, для которого функция Z = 10 x 1 + 5 x 2 (27.2) достигает наибольшего значения. Добавляя к левой части равенства (1) некоторую неотрицательную величину
называемую выравнивающей или базисной переменной, превратим их в уравнения (27.4):
При этом можно показать, что каждому решению системы неравенств (27.1) соответствует единственное решение системы уравнений (27.4) и неравенств (27.3) и наоборот. Каждая из переменных y 1, y 2, y 3 входит только в одно уравнение и зависит от переменных x 1 и x 2, которые мы называем свободными. Системе (27.4) соответствует исходное допустимое базисное решение x 1 = x 2 = 0; y 1 = 350; y 2 = 392; y 3 = 408 и Z = 0. Выполняем первое тождественное преобразование системы уравнений (27.4). Выбираем разрешающий столбец, соответствующий наименьшему отрицательному элементу в Z -строке, ибо теоретически установлено, что при этом можно ожидать при прочих равных условиях большего увеличения функции Z. Правую часть уравнений делим на элементы разрешающего столбца и выбираем наименьшее положительное отношение, соответствующее разрешающей строке (уравнению). На пересечении выделенных столбца и строки стоит разрешающее число. Первое уравнение делим на разрешающее число и выписываем получившееся уравнение. Умножая это уравнение на 14, 6 и –10 и вычитая соответственно из 2-го, 3-го и 4-го уравнений системы (27.4), придём к следующей системе (27.5):
Подобное тождественное преобразование, при котором выбор разрешающего числа производится по указанному правилу, будем называть симплексным преобразованием. Итак, симплексное преобразование выполняется по следующему правилу: 1. Выбирается разрешающий столбец, соответствующий наименьшему отрицательному элементу в Z -строке. 2. Выбирается разрешающая строка, которая соответствует наименьшему положительному из отношений элементов правой части уравнений на соответствующие элементы разрешающего столбца. На пересечении разрешающего столбца и разрешающей строки стоит разрешающее число. 3. Элементы разрешающей строки делятся на разрешающее число. 4. Вычисляются элементы всех остальных строк по формуле:
Из системы (27.5) находим второе допустимое базисное решение x 2 = y 1 = 0; x 1 = 25; y 2 = 42; y 3 = 258, которому соответствует новое увеличенное значение функции Z = 250. Таким образом, процесс последовательных симплексных преобразований является процессом последовательного улучшения решения. При этом: 1. Если в Z -строке найдётся хотя бы один отрицательный элемент и a) в разрешающем столбце найдётся хотя бы один положительный элемент, то можно улучшить решение; b) если же разрешающий столбец не содержит положительных элементов, то функция Z неограниченно возрастает. 2. Если все элементы в Z -строке неотрицательны, то достигнуто оптимальное решение. Это и есть достаточные условия существования оптимального плана решения. В системе (27.5) коэффициент при x 2 в Z -строке отрицательный, поэтому второй столбец будет разрешающим. Находим, что вторая строка будет разрешающей. Далее производим симплексное преобразование системы (27.5) согласно указанному правилу:
Так как в Z -строке все элементы неотрицательны, то данный план является оптимальным. При этом y 1 = y 2 = 0; x 1 = 20; x 2 = 14 и Z max = 270. [kgl].
[gl] Тема 28. Простейшие свойства комплексных чисел. Алгебраическая и тригонометрическая формы комплексных чисел [:] Величина вида z = x + iy (где x и y вещественные числа, которые составляют вещественную и мнимую части; i – мнимая единица) называются комплексными числами. Они получаются прежде всего при решении алгебраических уравнений: уже сама мнимая единица, очевидно, есть корень уравнения x 2 = –1. Часто используются обозначения x = Re(z), y =Im(z). Комплексное число на координатной плоскости (рисунок 28.1) представляется точкой M с координатами x, y; эту точку называют также изображением комплексного числа. И обратно, пару чисел x, y, образующих комплексное число z, называют аффиксом точки M.
Рисунок 28.1 – Изображение комплексного числа Здесь можно говорить о векторе z = r ·(cos φ + i ·sin φ) Запись z = r ·(cos φ + i ·sin φ) называется тригонометрической формой комплексного числа. r и φ можно найти по формулам
Запись числа z в виде z = x + iy называется алгебраической формой комплексного числа. Алгебраические действия с комплексными числами производятся по обычным правилам алгебры с учётом соотношения i 2 = –1. При сложении двух комплексных чисел z 1 = x 1 + iy 1 и z 2 = x 2 + iy 2: z = z 1 + z 2 = (x 1 + x 2) + i ·(y 1 + y 2). Пусть точки M 1, M 2 и M – изображения чисел z 1, z 2 и z. Из рисунка 28.2 видно, что точка M может быть получена по точкам M 1 и M 2 с помощью правила параллелограмма. Следовательно, сложение комплексных чисел z 1 и z 2 графически представляется как геометрическая сумма отрезков OM 1 и OM 2. Если r 1 и r 2 обозначают модули z 1 и z 2, то из рисунка 28.2 непосредственно следует справедливость двух неравенств: | z 1 + z 2| ≤ r 1 + r 2, | z 1 – z 2| ≥ | r 1 – r 2|.
Риснок 28.2 – Сложение двух комплексных чисел Произведение комплексного числа z на положительное вещественное число k, z 1 = k · z, представляет собой вектор, направленный туда же, куда направлен вектор z, но его модуль (длина) равен k · r, где r – модуль числа z. Если же k – отрицательное число, то вектор k · z имеет модуль | k |· r, но направлен противоположно вектору z. Легко построить также произведение z 1 комплексного числа z = x + iy на мнимую единицу i. Пусть отрезок OM представляет собой комплексное число x + iy. Имеем z 1 = i ·(x + iy) = – y + ix. Из рисунка 28.3 легко убедиться, что отрезок OM 1, изображающий комплексное число – y + ix = i ·(x + iy), представляет собой отрезок OM, повёрнутый вокруг начала координат на угол 90 º. Произведение комплексных чисел находится по простой формуле
Пусть точки M 1 и M 2 изображают два комплексных числа z 1 и z 2. Произведением этих двух чисел называют комплексное число, изображение которого M получается следующим способом (рисунок 28.4): выбирают точку G на оси абсцисс Ox таким образом, чтобы OG = 1, и строят подобные треугольники OGM 1 и OM 2 M. Из рисунка 28.4 видно, что модуль произведения равен произведению сомножителей: (OM) = (OM 1)·(OM 2) и что аргумент произведения равен сумме аргументов сомножителей:
В тригонометрической форме:
так что при перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. В частности, если есть n множителей и все они одинаковые, то имеет место возведение комплексного числа в натуральную степень
Последняя формула называется формулой Муавра. Замечание: одно комплексное число не может быть больше или меньше другого, т. е. их нельзя сравнивать. Тот же приём, выполняемый в обратном порядке, позволяет осуществить графически деление комплексных чисел. Очевидно, модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.
Рисунок 28.3 – Умножение комплексного числа Рисунок 28.4 – Умножение двух на (– i) комплексных чисел
Для алгебраической формы комплексного числа формула деления имеет вид
Для тригонометрической формы комплексного числа
При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются. При переходе от алгебраической формы комплексного числа к тригонометрической следует иметь в виду, что φ = Arg z = arg z + 2 k ·π, и
Поэтому достаточно определить лишь главное значение аргумента комплексного числа z, т. е. считать φ = arg z. Так как –π < arg z ≤ π, то из формулы
Если точка z лежит на действительной или мнимой оси, то arg z можно найти непосредственно. Например, arg z 1 = 0 для z 1 = 2; arg z 2 = π для z 2 = –3; arg z 3 = Сопряжённые комплексные числа Два комплексных числа, отличающихся только знаком мнимой части, называются сопряжёнными. Будем число, сопряжённое к комплексному числу z, обозначать через z *. Тогда если z = x + iy, то z * = x – iy. В частности, для вещественных чисел и только для них справедливо соотношение A * = A, так как в этом случае мнимая часть равна нулю. Для чисто мнимых чисел (т. е. чисел с равной нулю вещественной частью) и только для них справедливо соотношение A * = – A. При сложении двух комплексных чисел z 1 = x 1 + iy 1 и z 2 = x 2 + iy 2: z = z 1 + z 2 = (x 1 + x 2) + i ·(y 1 + y 2). Найдём теперь сумму сопряжённых чисел z 1* = x 1 – iy 1 и z 2* = x 2 – iy 2: z 1* + z 2* = (x 1 + x 2) – i ·(y 1 + y 2). Мы получили комплексное число, являющееся сопряжённым по отношению к сумме z 1 + z 2. Таким образом, если z 1 + z 2 = w, то z 1* + z 2* = w *, т. е. если слагаемые в сумме заменить на сопряжённые, то и сумма заменится на сопряжённую. Аналогичное свойство справедливо и для произведения комплексных чисел, т. е. если z 1· z 2 = w, то z 1*· z 2* = w *. Если Геометрически комплексное число z *, сопряжённое к z, изображается точкой M * – зеркальным образом относительно действительной оси Ox.
[kgl].
[gl] Тема 29. Формула Эйлера. Извлечение корня из комплексных чисел [:] Рассмотрим разложение в степенной ряд (ряд Тейлора) функции e iy :
В вещественной и мнимой части этого разложения можно узнать ряды для cos y и sin y. Таким образом, получаем формулу Эйлера: e iy = cos y + i ·sin y. Если заменить y на (– y), то e – iy = cos y – i ·sin y. Складывая и вычитая полученные формулы, найдём:
Отметим важные частные случаи формулы Эйлера:
Формула Эйлера даёт возможность комплексное число z = x + iy = r ·(cos φ + i ·sin φ) записать в виде z = r · e i φ. e i ·π + 1 = 0. Такая запись называется показательной формой комплексного числа. Последняя формула непосредственно иллюстрирует правило умножения и деления двух комплексных чисел z 1 = r 1· e i φ1, z 2 = r 2· e i φ2. В самом деле, имеем
Извлечение корня из комплексных чисел. Пусть n – натуральное число. Корнем n -й степени из комплексного числа ω = ρ·(cos θ + i ·sin θ) называется комплексное число z = r ·(cos φ + i ·sin φ), для которого zn = ω. Обозначим его По определению rn ·[cos (n ·φ) + i ·sin (n ·φ)] = ρ·(cos θ + i ·sin θ). Два комплексных числа в тригонометрической форме могут быть равны только тогда, когда равны их модули, а аргументы отличаются на целое кратное 2π: rn = ρ; n ·φ = θ + 2π· k, откуда
Следовательно,
Давая k значения 0, 1, 2, …, (n – 1), получим n различных значений корня. Для значений k = n, n + 1, … или k = –1, –2, … и т. д. значения корней будут повторять полученные ранее значения. Например, при k = 0 имеем
Пример 29.1. Найти значения
|

 0
0
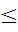 18
18
 0
0
 (27.1)
(27.1) , (27.3)
, (27.3)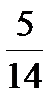 x 2
x 2
 y 1
y 1
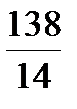 x 2
x 2
 y 1
y 1
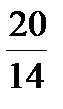 x 2
x 2
 y 1
y 1
 y 1
y 1
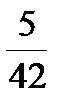 y 2
y 2
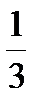 y 1
y 1
 y 2
y 2
 y 1
y 1
 y 2
y 2
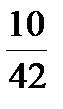 y 1
y 1
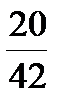 y 2
y 2
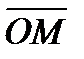 , изображающий комплексное число z. Положение точки на плоскости можно характеризовать её расстоянием от начала координат r и углом φ между вектором
, изображающий комплексное число z. Положение точки на плоскости можно характеризовать её расстоянием от начала координат r и углом φ между вектором  (например, для числа 5 i) или
(например, для числа 5 i) или  (например, для числа –5 i). Как видно из рисунка 28.1, x = r ·cos φ, y = r ·sin φ, так что можно выразить z через r и φ:
(например, для числа –5 i). Как видно из рисунка 28.1, x = r ·cos φ, y = r ·sin φ, так что можно выразить z через r и φ: .
.
 .
. ,
,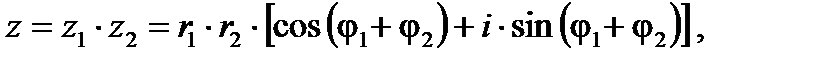
 .
. .
. .
. .
. получаем, что
получаем, что
 для z 3 = i; и arg z 4 =
для z 3 = i; и arg z 4 =  для z 4 = –8 i.
для z 4 = –8 i. , то
, то 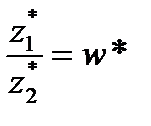 .
.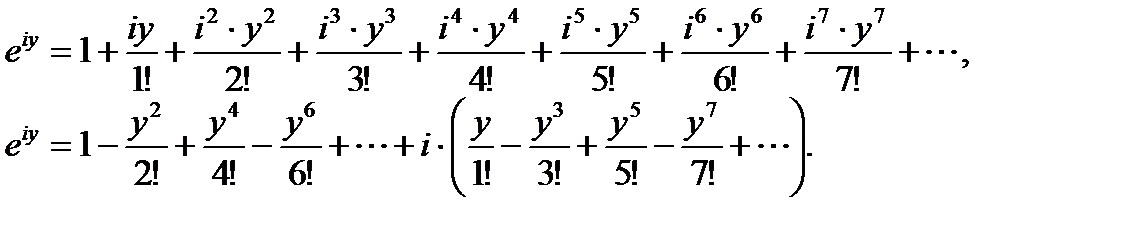
 .
.
 .
. .
.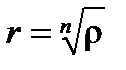 ,
,  .
.
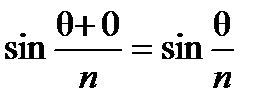 . При k = n имеем
. При k = n имеем 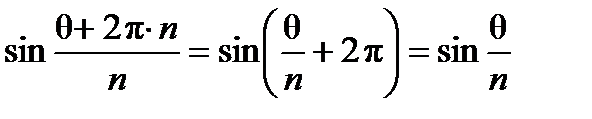 и т. д.
и т. д. .
.


