Решение. Запишем подкоренное выражение в тригонометрической форме:
Запишем подкоренное выражение в тригонометрической форме: i = 1·(cos 90º + i ·sin 90º). Стало быть,
ω k = cos[(90º + 360º· k)/5] + i ·sin[(90º + 360º· k)/5], k = 0, 1, 2, 3, 4. При k = 0 имеем ω0 = cos[(90º + 0º)/5] + i ·sin[(90º + 0º)/5] = cos 18º + i ·sin 18º или
При k = 1 имеем ω0 = cos[(90º + 360º)/5] + i ·sin[(90º + 360º)/5] = cos 90º + i ·sin 90º или
При k = 2 имеем ω0 = cos[(90º + 720º)/5] + i ·sin[(90º + 720º)/5] = cos 162º + i ·sin 162º или
При k = 3 имеем ω0 = cos[(90º + 1080º)/5] + i ·sin[(90º + 1080º)/5] = cos 234º + i ·sin 234º или
При k = 4 имеем ω0 = cos[(90º + 1440º)/5] + i ·sin[(90º + 1440º)/5] = cos 306º + i ·sin 306º или
Получили пять корней (рисунок 29.1, b). Из рисунка 29.1 a, b видно, что изображения этих корней совпадают с вершинами правильного многоугольника с n сторонами, вписанного в окружность, радиус которой равен единице, т. е. модулям данных комплексных чисел.
Рисунок 29.1 – Изображение корней: a) 2-ой степени; b) 5-ой степени
[kgl].
[gl] Тема 30. Показательная и логарифмическая функции. Другие элементарные функции комплексного переменного [:] Из формулы Эйлера
С другой стороны, для любых z 1 и z 2 справедливы формулы:
(теорема сложения для показательной функции);
Функция ez является периодической с периодом 2π· i. Область значений W охватывает всю плоскость, кроме её начала – точки O. Область однозначности функции ez Натуральный логарифм. Функция, обратная функции w = e z в области её однозначности, называется главной ветвью натурального логарифма:
Обратное отображение натуральной показательной функции во всей комплексной плоскости обозначают Ln z: если
Таким образом, Ln z состоит из множества ветвей функции:
Пример 30.1. Найти следующие логарифмы: ln(–1), Ln 1, ln i, ln (– i).
|

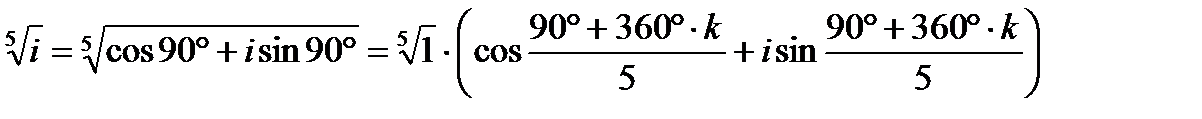 или
или ;
; ;
; ;
; ;
;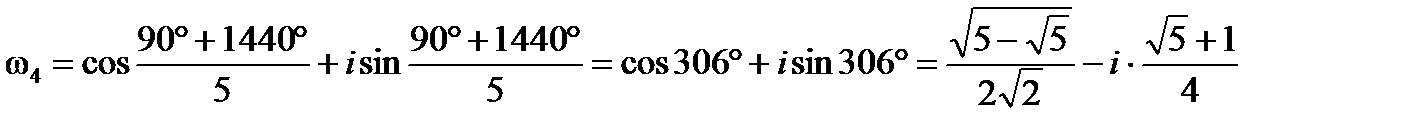 .
.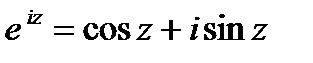 следует представление для ez:
следует представление для ez: .
.
 .
. есть вся плоскость, разрезанная вдоль отрицательной части действительной оси.
есть вся плоскость, разрезанная вдоль отрицательной части действительной оси. .
. , то
, то .
. .
.


