Обратные тригонометрические и гиперболические функции
Обратные тригонометрические функции обозначаются Arcsin z, Arccos z, Arctg z и определяются следующим образом: w = Arcsin z, если sin w = z; w = Arccos z, если cos w = z и w = Arctg z, если tg z = z. Как известно, тригонометрические функции выражаются через показательную функцию, поэтому естественно ожидать, что функции, обратные тригонометрическим, будут выражаться через логарифм. Действительно, по определению w = Arcsin z, если sin w = z или
откуда получаем:
Решая это квадратное уравнение относительно e i · w, имеем:
или, что то же,
Все значения функции Arcsin z определяются этим равенством. Аналогично получаются выражения через логарифм для функций: Arccos z и Arctg z.
Так как выражения, записанное под знаком логарифма, отличны от нуля, то функции Arcsin z и Arccos z определены при всех значениях z. Arcsin z и Arccos z – бесконечнозначные функции, что объясняется двузначностью квадратного корня и бесконечнозначностью логарифма. Arctg z – бесконечнозначная функция (за счёт логарифма), определённая при всех значениях z, кроме z = ± i. Обратные гиперболические функции обозначаются Arsh z (ареасинус z), Arch z (ареакосинус z), Arth z (ареатангенс z) и определяются следующим образом: w = Arsh z, если sh w = z; w = Arch z, если ch w = z и w = Arth z, если th z = z. Найдём выражения этих функций через логарифм. По определению w = Arsh z, если Таким образом, Arsh z – бесконечнозначная функция, определённая при всех значениях z. Она бесконечнозначна за счёт двузначности квадратного корня и бесконечнозначности логарифма. По определению w = Arch z, если
И, наконец, если w = Arth z, то Функция Arth z бесконечнозначная (за счёт логарифма), определённая при всех значениях z ≠ ±1.
[kgl].
|

 ,
, .
. ,
, 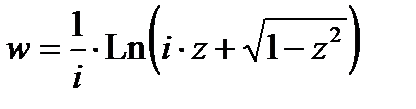
 .
. ,
,  .
. или
или  , откуда
, откуда  и, следовательно,
и, следовательно,  .
. , и, проведя аналогичные рассуждения, получим:
, и, проведя аналогичные рассуждения, получим: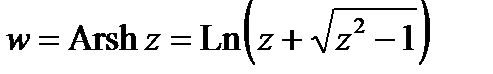 .
. , и, следовательно, можно получить:
, и, следовательно, можно получить:  .
.


