Основная задача линейного программированияЭта задача формулируется следующим образом. Дана линейная форма (целевая функция) Z = c 1· x 1 + c 2· x 2 + ·· + cn · xn (25.4) и задана система m > n линейных неравенств (ограничений)
причём, Нужно найти максимальное (минимальное) значение функции (25.4) при выполнении условий (25.5) и (25.6). [kgl].
[gl] Тема 26. Графический метод решения задач ЛП. Линии уровня целевой функции [:]
Свойства основной задачи линейного программирования связаны со свойствами выпуклых множеств. Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит и их произвольную выпуклую комбинацию. Геометрический смысл этого определения состоит в том, что множеству вместе с его произвольными точками полностью принадлежит и прямолинейный отрезок, их соединяющий. Примерами выпуклых множеств являются прямолинейный отрезок, полуплоскость, круг, шар, куб, полупространство и др. (рисунок 26.1) Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой комбинацией двух произвольных точек множества. Например, угловыми точками треугольника являются его вершины, круга – точки окружности, которые его ограничивают. Множество планов основной задачи линейного программирования является выпуклым (если оно не пусто). Непустое множество планов называется многогранником решений, а всякая угловая точка многогранника решений – вершиной.
Рисунок 26.1 – Примеры выпуклых и невыпуклых множеств Если основная задача линейного программирования имеет оптимальный план, то целевая функция задачи принимает максимальное значение в одной из вершин многогранника решений. Если максимальное значение достигается более чем в одной вершине, то целевая функция принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин. Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник, каждая вершина которого определяет опорный план. Для одного из опорных планов (т. е. в одной из вершин многогранника решений) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов). Вершину многогранника решений, в которой целевая функция принимает максимальное значение, можно найти достаточно просто, если задача в стандартной форме содержит не более двух переменных:
при условиях
Пересечение полуплоскостей, определяемое системой линейных неравенств, называется областью решений (OP) системы, а если она удовлетворяет условиям неотрицательности xj ≥ 0, то называется областью допустимых решений (ОДР). Если система неравенств совместна, то областью допустимых решений задачи является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств знаками точных равенств. Перед тем, как описать алгоритм нахождения максимума (минимума) целевой функции, введём понятие линии уровня и опорной прямой. Линией уровня называется прямая, на которой целевая функция принимает постоянное значение. Уравнение линии уровня в общем случае имеет вид
где c – константа. Все линии уровня параллельны между собой. Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с ОДР. Решение задачи линейного программирования геометрическим методом включает следующие этапы. 1. На плоскости x 1 Ox 2 строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств знаками точных равенств. 2. Находят полуплоскости, определяемые каждым из ограничений. 3. Строят многоугольник решений. 4. Строят вектор-градиент 5. Строят начальную прямую целевой функции 6. Определяют координаты вершины многоугольника, где целевая функция достигает максимума. Эта вершина (или точка) лежит на пересечении двух прямых, поэтому для нахождения её координат необходимо решить систему двух линейных уравнений, определя-ющих эти прямые. 7. Найденные значения Минимальное значение линейной функции цели находится путём передвижения начальной прямой
Пример 26.1. Найдите максимум линейной функции Z = 2 x 1 + 3 x 2 → max при условиях-ограничениях:
|
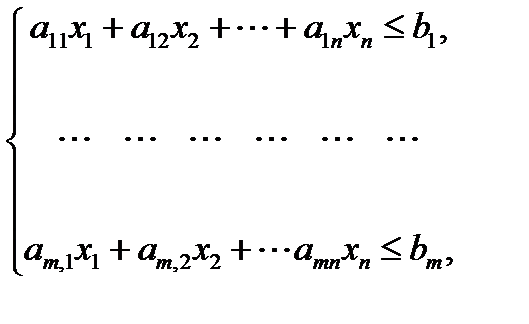(25.5)
(25.6)
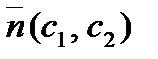, где c 1 и c 2 – коэффициенты соответственно перед переменными x 1 и x 2 в уравнении целевой функции 
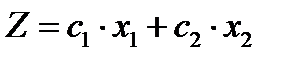. Вектор-градиент 
будет показывать направление перемещения линии уровня в сторону возрастания значения целевой функции. Мысленно перемещая линию уровня в направлении до тех пор, пока она не будет иметь одну общую точку с ОДР, находим вершину, где целевая функция достигает максимума.
. Эта прямая пройдёт через начало координат. Чтобы построить её перепишем уравнение в виде y = kx + b. Это – уравнение прямой линии с угловым коэффициентом k и начальной ординатой b. В нашем случае начальная ордината b = 0 и уравнение перепишется в виде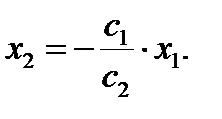 
Здесь угловой коэффициент 
. Затем передвигают её параллельно самой себе в направлении вектора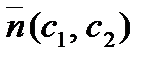 
до крайней угловой точки многоугольника решений. В результате находят точку, в которой целевая функция принимает максимальное значение, либо множество точек с одинаковым максимальным значением целевой функции альтернативный оптимум, если начальная прямая сливается с одной из сторон многоугольника решений, либо устанавливают неограниченность сверху функции на множестве планов 
.
и 
образуют набор переменных управления, которые обеспечивают максимально (минимально) возможное значение целевой функции. Вычисляют значение целевой функции в этой точке: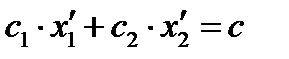 
.
.
