| | §1 Виды уравнений плоскости
| |
| | 1. Уравнение плоскости, проходящей через три точки
|
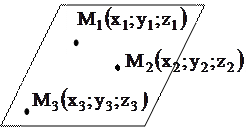 Уравнение плоскости, проходящей через три точки
Уравнение плоскости, проходящей через три точки 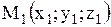 , , 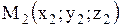 , , 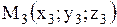
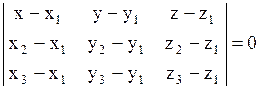
| |
| | 2. Уравнение плоскости, проходящей через точку с нормальным вектором
| 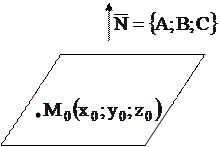 Уравнение плоскости, проходящей через точку
Уравнение плоскости, проходящей через точку  с нормальным вектором с нормальным вектором 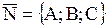
 (нормальный вектор – вектор, перпендикулярный плоскости)
(нормальный вектор – вектор, перпендикулярный плоскости)
| |
| | 3. Уравнение плоскости в отрезках
|
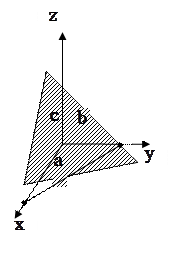 Уравнение плоскости в отрезках
Уравнение плоскости в отрезках
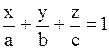 ,
где ,
где  отрезки, которые отсекает плоскость соответственно на осях отрезки, которые отсекает плоскость соответственно на осях 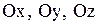 . .
| Задача.
Какие отрезки отсекает плоскость 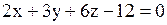 на осях координат.
Решение.
Сведем к уравнению плоскости в отрезках на осях координат.
Решение.
Сведем к уравнению плоскости в отрезках
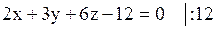 , ,
 .
Тогда по оси Ох отсекается отрезок, равный 6; по оси Оу – отрезок, равный 4; по оси Оz – отрезок, равный 2. .
Тогда по оси Ох отсекается отрезок, равный 6; по оси Оу – отрезок, равный 4; по оси Оz – отрезок, равный 2.
| |
| | 4. Общее уравнение плоскости
| 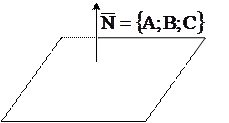 Общееуравнение плоскости
Общееуравнение плоскости
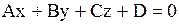 Коэффициенты при переменных x, y и z – это координаты нормального вектора
Коэффициенты при переменных x, y и z – это координаты нормального вектора 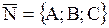 . .
| Задача.
Нормальный вектор плоскости 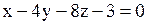 имеет координаты
Варианты ответов: 1) имеет координаты
Варианты ответов: 1) 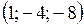 2)
2) 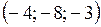 3) 3)  4)
4) 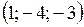 Решение.
Координаты нормального вектора – это коэффициенты при переменных
Решение.
Координаты нормального вектора – это коэффициенты при переменных 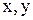 и и  . .  Ответ. №1.
Ответ. №1.
| |
| | Задача.
Плоскости 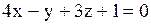 принадлежат точки…
Варианты ответов: 1) принадлежат точки…
Варианты ответов: 1)  2) 2)  3) 3) 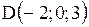 4) 4) 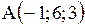 Решение.
Точка принадлежит плоскости, если ее координаты удовлетворяют уравнению плоскости.
С:
Решение.
Точка принадлежит плоскости, если ее координаты удовлетворяют уравнению плоскости.
С: 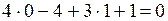 . С принадлежит плоскости
Е: . С принадлежит плоскости
Е: 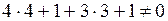 D:
D: 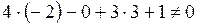 А:
А: 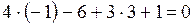 . А принадлежит плоскости
Ответ. точки С и А принадлежат плоскости.
Задача.
Если точка . А принадлежит плоскости
Ответ. точки С и А принадлежат плоскости.
Задача.
Если точка  принадлежит плоскости принадлежит плоскости  , то коэффициент С равен…
Решение.
Подставим координаты точки в уравнение плоскости , то коэффициент С равен…
Решение.
Подставим координаты точки в уравнение плоскости

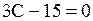
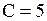 Ответ.
Ответ. 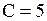
| |
| §2 Частные случаи общего уравнения плоскости
|
5. Плоскость 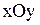
|  Плоскость (xOy):
Плоскость (xOy): 
| Задача:
Установить соответствие между уравнением плоскости и ее положением в пространстве.
1) 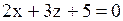 2)
2)  3)
3) 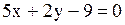 4)
4)  Варианты ответов: А) параллельна оси
Варианты ответов: А) параллельна оси  В) проходит через начало координат
С) параллельна оси
В) проходит через начало координат
С) параллельна оси 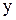 D) проходит через ось
D) проходит через ось 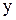 Е) параллельна оси
Е) параллельна оси 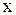 Решение.
1)
Решение.
1) 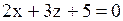 .
Отсутствует переменная .
Отсутствует переменная 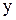 . Тогда параллельна оси . Тогда параллельна оси 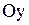 .
2) .
2)  . Отсутствует переменная . Отсутствует переменная 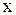 . Тогда параллельна оси . Тогда параллельна оси 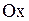 .
3) .
3) 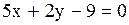 . Отсутствует переменная . Отсутствует переменная  . Тогда параллельна оси . Тогда параллельна оси 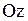 .
4) .
4) 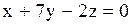 . Отсутствует свободный член. Тогда плоскость проходит через начало координат. . Отсутствует свободный член. Тогда плоскость проходит через начало координат.
|
6. Плоскость 
|  Плоскость (xOz):
Плоскость (xOz): 
|
7. Плоскость 
| 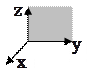 Плоскость (yOz):
Плоскость (yOz): 
|
8. Плоскость, параллельная 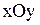
|  Плоскость, параллельная (xOy): Плоскость, параллельная (xOy):
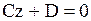 или или 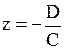 (в уравнении отсутствуют переменные
(в уравнении отсутствуют переменные 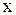 и и 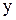 ) )
|
9. Плоскость, параллельная 
| 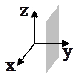 Плоскость, параллельная (xOz): Плоскость, параллельная (xOz):
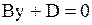 или или 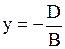 (в уравнении отсутствуют переменные
(в уравнении отсутствуют переменные 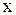 и и  ) )
|
10. Плоскость, параллельная 
| 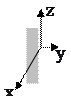 Плоскость, параллельная (yOz): Плоскость, параллельная (yOz):
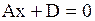 или или 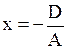 (в уравнении отсутствуют переменные
(в уравнении отсутствуют переменные 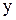 и и  ) )
|
| 11. Плоскость проходит через начало координат
|  Плоскость проходит через начало координат Плоскость проходит через начало координат
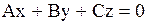
|
12. Плоскость, параллельная оси 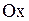
|  Плоскость, параллельная оси Ox: Плоскость, параллельная оси Ox: 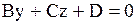 (в уравнении отсутствует переменная
(в уравнении отсутствует переменная 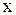 ) )
| Ответ. 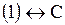 
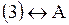 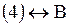
|
13. Плоскость, параллельная оси 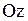
| 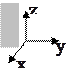 Плоскость, параллельная оси Oz: Плоскость, параллельная оси Oz:
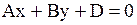 (в уравнении отсутствует переменная
(в уравнении отсутствует переменная  ) )
|
14. Плоскость, параллельная оси 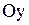
|  Плоскость, параллельная оси Oy: Плоскость, параллельная оси Oy: 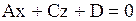 (в уравнении отсутствует переменная
(в уравнении отсутствует переменная 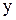 ) )
|
| 15. Расстояние от точки до плоскости
| Расстояние от точки  до плоскости до плоскости 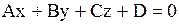 вычисляется пор формуле вычисляется пор формуле
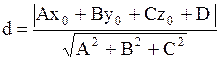
|
§3 Взаимное расположение плоскостей
Пусть даны плоскости 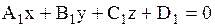 и и 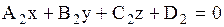
|
| 16. Условие
перпендикулярности плоскостей
| 
| Задача.
Найти угол между плоскостями 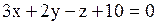 и и 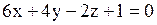 .
Решение.
Нормальный вектор плоскости .
Решение.
Нормальный вектор плоскости 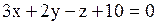 имеет координаты имеет координаты 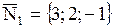 . Для второй плоскости . Для второй плоскости 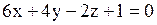 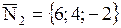 . Воспользуемся формулой вычисления угла . Воспользуемся формулой вычисления угла
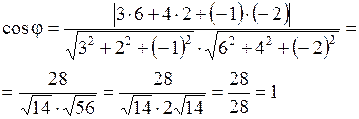
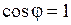 , , 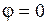 .
Ответ. .
Ответ. 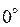 . .
|
| 17. Условие
параллельности плоскостей
| 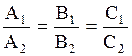
|
| 18. Угол между плоскостями
| 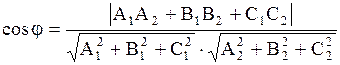
|
| | | | | | | | | |