Основные методы интегрирования
| 1. Непосредственное интегрирование
| 1)  , , 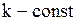 2)
2)  3)
3) 
| а)  
 б)
б) 
| | 2. Внесение функции под знак дифференциала
| | Таблица дифференциалов
|
а)  б)
б) 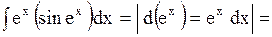
 в)
в)  
| 1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6.  7.
7.  8.
8. 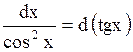
| 9.  10.
10.  11.
11.  12.
12.  13.
13.  14.
14. 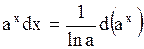 . .
| | | | | |
3. Правило подстановки 
| Подстановка 
| а) 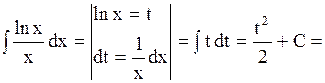  б)
б) 

| 4. Интегрирование по частям 
| 1)  2) 2)  3)
3) 
| а) 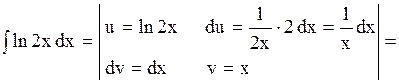
 б)
б) 
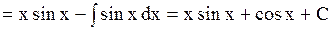
| | | | |
| 5. Интегрирование простейших дробей
| 1)  2)
2)  3)
3) 
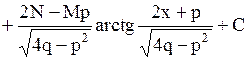
| а)  б)
б) 
 в)
в)  

 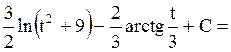
 . .
| | 6. Интегрирование рациональных дробей
| | 1. Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби (выделить целую часть).
2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей.
|  Дробь
Дробь  правильная. Представим ее в виде суммы простейших дробей: правильная. Представим ее в виде суммы простейших дробей:
 , приведем к общему знаменателю , приведем к общему знаменателю
|
| 3. Проинтегрировать многочлен и полученную сумму простейших дробей.
| 
 ; ;
 приравняем коэффициенты при одинаковых степенях х:
приравняем коэффициенты при одинаковых степенях х:
 ; ; 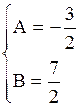 Значит:
Значит:

| | 7. Интегрирование тригонометрических функций
| 7.1. 


| Необходимо преобразовать произведение тригонометрических функций в сумму или разность, пользуясь одной из следующих формул

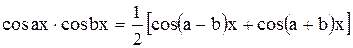

|
а) 

| 7.2. 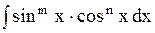 ,
где ,
где  и и  - целые числа - целые числа
|
Если m – нечетное положительное, то подстановка  .
Если n – нечетное положительное, то подстановка .
Если n – нечетное положительное, то подстановка  .
Если .
Если  - четное отрицательное, то подстановка - четное отрицательное, то подстановка  .
Если .
Если  и и  - четные неотрицательные, то применяются формулы: - четные неотрицательные, то применяются формулы:
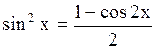 ; ; 
| б) 

|
7.3. 
| Универсальная подстановка  , тогда , тогда
 ; ; 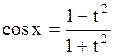 ; ;
 ; ;  .
Если .
Если  , то подстановка , то подстановка  ;
Если ;
Если  , то подстановка , то подстановка  ;
Если ;
Если  , то подстановка , то подстановка  . .
| в) 
  
| | | | | |
| 8. Интегрирование иррациональных функций
|
8.1.  8.2.
8.2.  8.3. Квадратичные
иррациональности
8.3. Квадратичные
иррациональности


 8.4. Интегралы типа
8.4. Интегралы типа
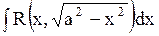

 8.5. Дифференциальный
бином
8.5. Дифференциальный
бином
 ,
где ,
где
 - рациональные числа,
а, b – действительные числа - рациональные числа,
а, b – действительные числа
|
Приводится к интегралу от рациональной дроби подстановкой  , где , где  - наименьшее общее кратное знаменателей дробей - наименьшее общее кратное знаменателей дробей  Сводится к интегралу от рациональной дроби подстановкой
Сводится к интегралу от рациональной дроби подстановкой  Под радикалом выделить полный квадрат
Под радикалом выделить полный квадрат
 и сделать подстановку и сделать подстановку  Подстановка
Подстановка  Подстановка
Подстановка  Подстановка
Подстановка  1-й случай
а) если р – целое положительное число, то нужно раскрыть скобки
1-й случай
а) если р – целое положительное число, то нужно раскрыть скобки  по биному Ньютона и вычислить интегралы от степеней;
б) если р – целое отрицательное число, то подстановка по биному Ньютона и вычислить интегралы от степеней;
б) если р – целое отрицательное число, то подстановка  , где , где  - наименьшее общее кратное знаменателей дробей m и n, приводит к интегралу от рациональной дроби;
2-й случай
если - наименьшее общее кратное знаменателей дробей m и n, приводит к интегралу от рациональной дроби;
2-й случай
если  - целое число, то применяется подстановка - целое число, то применяется подстановка 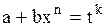 , где , где  - знаменатель дроби р;
3-й случай
если - знаменатель дроби р;
3-й случай
если  - целое число, то применяется подстановка - целое число, то применяется подстановка  , где , где  - знаменатель дроби - знаменатель дроби 
| 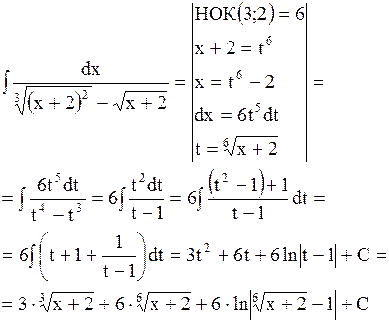
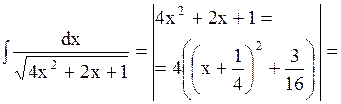

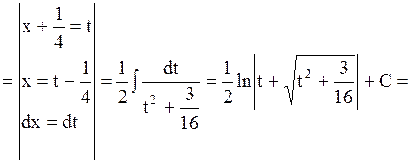







|
Задача.
Первообразными функции  являются
Варианты ответов: 1) являются
Варианты ответов: 1)  2) 2)  3) 3) 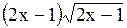 4) 4)  Решение.
Т.к.
Решение.
Т.к.  , то , то  , тогда , тогда  Ответ. №4
Задача.
Множество первообразных функции
Ответ. №4
Задача.
Множество первообразных функции  имеет вид
Варианты ответов: 1) имеет вид
Варианты ответов: 1)  2) 2)  3) 3)  4) 4)  Решение.
Решение.
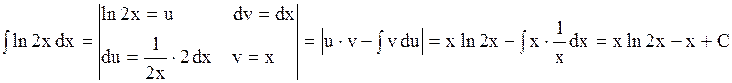 Ответ. №1
Задача.
В неопределенном интеграле
Ответ. №1
Задача.
В неопределенном интеграле  введена новая переменная введена новая переменная  . Тогда интеграл принимает вид
Варианты ответов: 1) . Тогда интеграл принимает вид
Варианты ответов: 1) 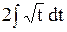 2) 2)  3) 3)  4) 4)  Решение.
Решение.
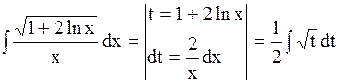 Ответ. №4
Задача.
Установите соответствие между интегралом и его значением
1.
Ответ. №4
Задача.
Установите соответствие между интегралом и его значением
1.  2. 2. 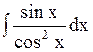 3. 3.  4. 4.  Варианты ответов: а)
Варианты ответов: а) 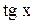 в) в) 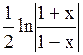 с) с)  d) d) 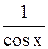 е) е) 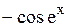 Решение.
1)
Решение.
1)  2)
2) 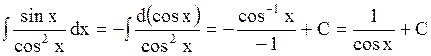 3)
3)  4) 4)  Ответ.
Ответ. 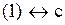  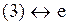 
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
Классификация холодных блюд и закусок. Урок №2 Тема: Холодные блюда и закуски. Значение холодных блюд и закусок. Классификация холодных блюд и закусок. Кулинарная обработка продуктов...
ТЕРМОДИНАМИКА БИОЛОГИЧЕСКИХ СИСТЕМ. 1. Особенности термодинамического метода изучения биологических систем. Основные понятия термодинамики. Термодинамикой называется раздел физики...
Травматическая окклюзия и ее клинические признаки При пародонтите и парадонтозе резистентность тканей пародонта падает...
|
Уравнение волны. Уравнение плоской гармонической волны. Волновое уравнение. Уравнение сферической волны Уравнением упругой волны называют функцию , которая определяет смещение любой частицы среды с координатами относительно своего положения равновесия в произвольный момент времени t...
Медицинская документация родильного дома Учетные формы родильного дома № 111/у Индивидуальная карта беременной и родильницы
№ 113/у Обменная карта родильного дома...
Основные разделы работы участкового врача-педиатра Ведущей фигурой в организации внебольничной помощи детям является участковый врач-педиатр детской городской поликлиники...
|
|