Глава 6. Кривые второго порядка
| Уравнение
| Чертеж
| Фокусы
| Эксцентриситет
| Директриса
| Асимптота
| 1. Эллипс
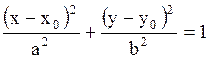
 - центр - центр
 - полуоси - полуоси
|  
| Если  

| 
| 
| –
| Если  

| 
| 
| –
| 2. Гипербола

 - центр - центр
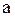 - действительная полуось, - действительная полуось,
 - мнимая - мнимая
|  
| 

| 
| 
| 
| 3. Гипербола
 или
или

 - центр - центр
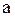 - мнимая полуось, - мнимая полуось,
 - действительная - действительная
| 
| 

| 
| 
| 
| 4. Парабола
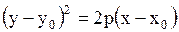
 - вершина - вершина
 - расстояние между фокусом и директрисой - расстояние между фокусом и директрисой
| 
| 
| -
| 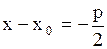
| -
| 5. Парабола

| 
| 
| -
| 
| -
| 6. Парабола
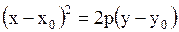
| 
| 
| -
| 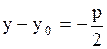
| -
| 7. Парабола

| 
| 
| -
| 
| -
| 8. Окружность

 - центр - центр
 - радиус - радиус
|  
| -
| 
| -
| -
| 9. Две пересекающиеся прямые

|
| -
| -
| -
| -
| 10. Уравнение
 определяет точку определяет точку 
| -
| -
| -
| -
| -
| Задача.
Укажите соответствие между кривыми второго порядка и их уравнениями:
1. 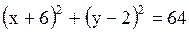 2. 2.  3. 3.  4. 4.  Варианты ответов: А) эллипс В) гипербола С) окружность D) парабола
Решение.
Проанализируем каждое уравнение
1). Уравнение можно записать в виде
Варианты ответов: А) эллипс В) гипербола С) окружность D) парабола
Решение.
Проанализируем каждое уравнение
1). Уравнение можно записать в виде  . Это уравнение окружности.
2). Уравнение содержит переменную . Это уравнение окружности.
2). Уравнение содержит переменную 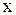 во второй степени, а переменную во второй степени, а переменную 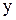 - в первой. Это уравнение параболы.
3). Поделим уравнение на 4. Тогда - в первой. Это уравнение параболы.
3). Поделим уравнение на 4. Тогда  . Обе переменные в квадрате. В левой части – сумма; в правой – единица. Это уравнение эллипса.
4). . Обе переменные в квадрате. В левой части – сумма; в правой – единица. Это уравнение эллипса.
4).  . Обе переменные во второй степени. В левой части – разность; в правой – единица. Это уравнение гиперболы.
Ответ. . Обе переменные во второй степени. В левой части – разность; в правой – единица. Это уравнение гиперболы.
Ответ. 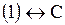 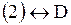 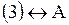  Задача.
Установите соответствие между кривой второго порядка и ее уравнением.
1. Парабола 2. Эллипс 3. Гипербола
Варианты ответов: А)
Задача.
Установите соответствие между кривой второго порядка и ее уравнением.
1. Парабола 2. Эллипс 3. Гипербола
Варианты ответов: А)  В) В)  С) С)  D) D)  Е) Е)  Решение.
1). Парабола. В уравнении одна переменная должна быть в первой степени, другая – во второй. Это уравнение (D).
2). Эллипс. Обе переменные должны быть во второй степени. В левой части – сумма; в правой – единица. Это уравнение (Е).
3). Гипербола. Обе переменные должны быть во второй степени. В левой части – разность; в правой – единица. Это уравнение (В)
Ответ.
Решение.
1). Парабола. В уравнении одна переменная должна быть в первой степени, другая – во второй. Это уравнение (D).
2). Эллипс. Обе переменные должны быть во второй степени. В левой части – сумма; в правой – единица. Это уравнение (Е).
3). Гипербола. Обе переменные должны быть во второй степени. В левой части – разность; в правой – единица. Это уравнение (В)
Ответ. 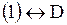  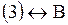 Задача.
Если
Задача.
Если  - центр окружности, которая проходит через точку - центр окружности, которая проходит через точку  , то уравнение этой окружности имеет вид…
Варианты ответов: 1) , то уравнение этой окружности имеет вид…
Варианты ответов: 1)  2) 2) 
 3) 3)  4) 4)  Решение.
Так как
Решение.
Так как  - центр, то уравнение может быть №3 или №4. Найдем радиус – это расстояние АС. - центр, то уравнение может быть №3 или №4. Найдем радиус – это расстояние АС.
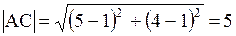 . Итак, . Итак,  , тогда уравнение №3.
Ответ. №3.
Задача.
Если уравнение гиперболы имеет вид , тогда уравнение №3.
Ответ. №3.
Задача.
Если уравнение гиперболы имеет вид  , то длина ее действительной полуоси равна…
Варианты ответов: 1) 3 2) 16 3) 9 4) 4
Решение.
Действительная полуось берется из положительного слагаемого , то длина ее действительной полуоси равна…
Варианты ответов: 1) 3 2) 16 3) 9 4) 4
Решение.
Действительная полуось берется из положительного слагаемого 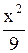 . Тогда . Тогда  , ,  .
Ответ. №1.
Задача.
Если уравнение окружности имеет вид .
Ответ. №1.
Задача.
Если уравнение окружности имеет вид  , то его центром С и радиусом r являются…
Варианты ответов: 1) , то его центром С и радиусом r являются…
Варианты ответов: 1)  , ,  2) 2)  , ,  3) 3)  , ,  4) 4)  , ,  Решение.
Уравнение можно записать в виде
Решение.
Уравнение можно записать в виде  . Тогда центр . Тогда центр  , радиус , радиус  .
Ответ. №2.
Задача.
Радиус окружности, заданной уравнением .
Ответ. №2.
Задача.
Радиус окружности, заданной уравнением  , равен …
Варианты ответов: 1) 3 2) -1 3) 4 4) 1
Решение. , равен …
Варианты ответов: 1) 3 2) -1 3) 4 4) 1
Решение.
 ; ;  . Тогда центр . Тогда центр  , радиус , радиус  .
Ответ. №4. .
Ответ. №4.
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Типовые ситуационные задачи. Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической
Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической нагрузке. Из медицинской книжки установлено, что он страдает врожденным пороком сердца....
Типовые ситуационные задачи. Задача 1.У больного А., 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт Задача 1.У больного А., 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт. ст. Влияние психоэмоциональных факторов отсутствует. Колебаний АД практически нет. Головной боли нет. Нормализовать...
Эндоскопическая диагностика язвенной болезни желудка, гастрита, опухоли Хронический гастрит - понятие клинико-анатомическое, характеризующееся определенными патоморфологическими изменениями слизистой оболочки желудка - неспецифическим воспалительным процессом...
|
Классификация ИС по признаку структурированности задач Так как основное назначение ИС – автоматизировать информационные процессы для решения определенных задач, то одна из основных классификаций – это классификация ИС по степени структурированности задач...
Внешняя политика России 1894- 1917 гг. Внешнюю политику Николая II и первый период его царствования определяли, по меньшей мере три важных фактора...
Оценка качества Анализ документации. Имеющийся рецепт, паспорт письменного контроля и номер лекарственной формы соответствуют друг другу. Ингредиенты совместимы, расчеты сделаны верно, паспорт письменного контроля выписан верно. Правильность упаковки и оформления....
|
|