| 1 Область определения функции нескольких переменных
|
Пусть даны два числовых множества 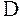 и и  , где , где  некоторая область из пространства некоторая область из пространства  , а , а  некоторое подмножество множества некоторое подмножество множества  . Если каждой паре чисел . Если каждой паре чисел  по некоторому правилу (закону) поставлено в соответствие единственное число по некоторому правилу (закону) поставлено в соответствие единственное число  , то говорят, что на множестве , то говорят, что на множестве 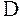 задана функция двух переменных задана функция двух переменных 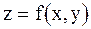 . При этом . При этом  и и  называются независимыми переменными (или аргументами), называются независимыми переменными (или аргументами),  зависимой переменной (или функцией), множество зависимой переменной (или функцией), множество  областью определения функции, а областью определения функции, а  множеством значений функции. множеством значений функции.
|
Задача.
Найти область определения функции  . .
Решение. Функция определена при условии  , т.е. , т.е.  . Это круг с центром в начале координат и радиусом 1, включающий свою границу, т.е. окружность . Это круг с центром в начале координат и радиусом 1, включающий свою границу, т.е. окружность  . .
|
| 2 Предел функции нескольких переменных
|
Число  называется пределом функции называется пределом функции  при при  , если для любого числа , если для любого числа  найдется такая найдется такая  окрестность точки окрестность точки 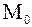 , что для любой точки , что для любой точки  из этой окрестности (за исключением, быть может, точки из этой окрестности (за исключением, быть может, точки 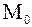 ) имеет место неравенство ) имеет место неравенство  .
При этом пишут .
При этом пишут  или или  , так как при , так как при  , очевидно , очевидно 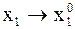 , ,  ,..., ,..., 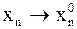 . .
| Задача.
Найти предел  .
Решение. .
Решение.

 .
Ответ. 2. .
Ответ. 2.
|
| 3 Частные производные функции нескольких переменных
|
Частной производной функции 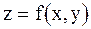 по переменной по переменной  , в точке , в точке  называется предел (если таковой существует) отношения частного приращения называется предел (если таковой существует) отношения частного приращения  к приращению аргумента к приращению аргумента  при стремлении последнего к нулю: при стремлении последнего к нулю:
 Аналогично определяется частная производная
Аналогично определяется частная производная
 Для обозначения частных производных функции двух переменных применяются следующие символы:
Для обозначения частных производных функции двух переменных применяются следующие символы:
 . .
| Задача.
Найти частные производные функции 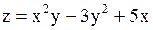 .
Решение. .
Решение.


|
| 4 Частные производные высших порядков
|
Пусть имеем некоторую функцию  от двух переменных от двух переменных  и и  . Ее частные производные . Ее частные производные  и и  являются функциями от переменных являются функциями от переменных  и и  . В некоторых случаях для этих функций существуют снова частные производные, называемые частными производными второго порядка (или просто вторыми частными производными): . В некоторых случаях для этих функций существуют снова частные производные, называемые частными производными второго порядка (или просто вторыми частными производными):
 , ,
 , ,
 , ,
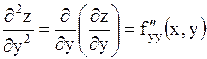 .
Теорема.Если в некоторой окрестности точки .
Теорема.Если в некоторой окрестности точки  производные производные  и и  существуют и непрерывны в самой точке существуют и непрерывны в самой точке  , то они равны между собой в этой точке, т.е. имеет место равенство: , то они равны между собой в этой точке, т.е. имеет место равенство:
 . .
| Задача.
Пусть  Имеем
Имеем 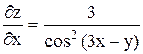 , ,
 , ,
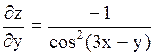 , ,

 , ,  . .
|
| 5 Производная сложной функции. Случай одной независимой переменной.
|
Теорема. Если функции  и и  дифференцируемы в точке дифференцируемы в точке 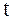 , а функция , а функция 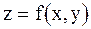 дифференцируема в соответствующей точке дифференцируема в соответствующей точке  , то сложная функция , то сложная функция  также дифференцируема в точке также дифференцируема в точке 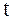 и имеет место формула и имеет место формула
 . .
| Задача.
Пусть  , где , где  .
Решение. .
Решение.
 . .
|
Если  , ,  . Тогда . Тогда  является сложной функцией переменной является сложной функцией переменной  , где , где
 . .
| Задача.
Пусть  , где , где  .
Решение. .
Решение.
  . .
|
| 6 Производная сложной функции. Случай нескольких независимых переменных.
|
Если функции  , ,  дифференцируемы в точке дифференцируемы в точке 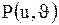 , а функция , а функция 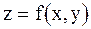 дифференцируема в точке дифференцируема в точке  , где , где  , ,  то сложная функция то сложная функция  дифференцируема в точке дифференцируема в точке 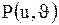 , причем ее частные производные в этой точке находятся по формулам , причем ее частные производные в этой точке находятся по формулам

| Задача.
Пусть 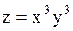 , ,  , ,  Решение.
Решение.

|
| 7 Полный дифференциал функции
|
Выражение  называется полным приращениемфункции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.
Полным дифференциаломфункции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у). называется полным приращениемфункции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.
Полным дифференциаломфункции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у).
 Для функции произвольного числа переменных:
Для функции произвольного числа переменных:

| Задача.
Найти полный дифференциал функции  . .



|
| 8 Производная неявно заданной функции
|
Если  - дифференцируемая функция переменных - дифференцируемая функция переменных  , , 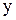 и и  в некоторой области D и в некоторой области D и  , то уравнение , то уравнение  определяет однозначно неявную функцию определяет однозначно неявную функцию  , также дифференцируемую, и , также дифференцируемую, и
 , , 
| Задача.
Найти производную неявной функции  , заданной уравнением , заданной уравнением 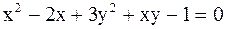 , и вычислить ее значение в точке , и вычислить ее значение в точке  .
Решение. Введем обозначение .
Решение. Введем обозначение  . Тогда . Тогда 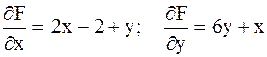 . Следовательно, . Следовательно,
 и и 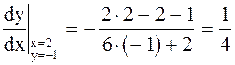 . .
|
| 9 Приближенные вычисления с помощью дифференциала
|
В приближенных вычислениях пользуются данной формулой.

| Задача.
Вычислить приближенно с помощью дифференциала  .
Решение.
Рассмотрим функцию .
Решение.
Рассмотрим функцию  . .
 или
или
 .
Положим теперь .
Положим теперь  ; тогда ; тогда
 . Следовательно, . Следовательно,
 .
Или .
Или  . .
|
| 10 Касательная плоскость к поверхности
|
Плоскость, проходящая через точку  , называется касательной плоскостью к поверхности в точке , называется касательной плоскостью к поверхности в точке  , если угол между секущей , если угол между секущей  и этой плоскостью стремится к нулю, когда расстояние и этой плоскостью стремится к нулю, когда расстояние  стремится к нулю, каким бы образом точка стремится к нулю, каким бы образом точка 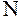 на поверхности ни стремилась к точке на поверхности ни стремилась к точке  . .
Уравнение касательной плоскости к поверхности в точке  , если плоскость задана неявно: , если плоскость задана неявно:
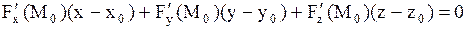
Уравнение касательной плоскости к поверхности в точке  , если плоскость задана явно: , если плоскость задана явно:
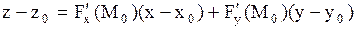
| Задача.
Найти уравнение касательной плоскости к сфере  в точке в точке  , где , где  .
Решение.
Подставляя .
Решение.
Подставляя  и и  в уравнение сферы, находим в уравнение сферы, находим  , т.е. , т.е.  . Запишем уравнение сферы в неявном виде: . Запишем уравнение сферы в неявном виде:  , откуда , откуда
 .
Найдем .
Найдем  , ,  , ,  .
Уравнение касательной плоскости: .
Уравнение касательной плоскости:  , или , или
 - плоскость параллельна оси - плоскость параллельна оси  . .
|
| 11 Нормаль к поверхности
|
Уравнение нормали в точке  к поверхности, заданной неявно, запишется в виде: к поверхности, заданной неявно, запишется в виде:
 .
Уравнение нормали в точке .
Уравнение нормали в точке  к поверхности, заданной явно, запишется в виде: к поверхности, заданной явно, запишется в виде:

| Задача.
Записать уравнения нормали к поверхности  в точке в точке  .
Решение.
Поскольку .
Решение.
Поскольку  , то , то
 , ,  .
Уравнение нормали: .
Уравнение нормали: 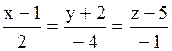 . .
|
| 12 Экстремум функции нескольких переменных
|
Алгоритм исследования функции  на экстремум
1) Проверить необходимое условие экстремума:
1. Найти частные производные первого порядка на экстремум
1) Проверить необходимое условие экстремума:
1. Найти частные производные первого порядка  2. Решив систему уравнений
2. Решив систему уравнений
 найти точки возможного экстремума.
2) Проверить достаточные условия экстремума:
1.Найти частные производные второго порядка
найти точки возможного экстремума.
2) Проверить достаточные условия экстремума:
1.Найти частные производные второго порядка  2. Составить матрицу
2. Составить матрицу  , где , где  , ,  , ,  . .
| Задача.
Исследовать на экстремум функцию
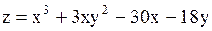 .
Решение.
Областью определения является вся плоскость .
Решение.
Областью определения является вся плоскость 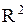 . Найдем критические точки. . Найдем критические точки.
 , ,  .
Приравнивая эти производные нулю, приходим к системе: .
Приравнивая эти производные нулю, приходим к системе:
 Решая эту систему уравнений, находим четыре критические точки
Решая эту систему уравнений, находим четыре критические точки
 .
Теперь найдем вторые частные производные: .
Теперь найдем вторые частные производные:  и составим выражение и составим выражение
 .
Тогда:
1) .
Тогда:
1) 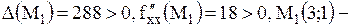 точка минимума;
2) точка минимума;
2) 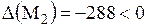 , в точке , в точке  экстремума нет;
3) экстремума нет;
3)  , в точке , в точке  экстремума нет;
4) экстремума нет;
4)   точка максимума.
Итак, данная функция имеет два экстремума: в точке точка максимума.
Итак, данная функция имеет два экстремума: в точке  минимум, минимум,  и в точке и в точке  максимум, максимум, 
|
| | | | | | | | | | | | |