Глава 3. Прямая на плоскости
| §1 Виды уравнений прямой на плоскости
| | 1. Уравнение прямой, проходящей через точку с нормальным вектором
| 
Уравнение прямой, проходящей через точку  с нормальным вектором 
(нормальный вектор – вектор, перпендикулярный прямой)
| Задача.
Даны вершины треугольника  ,  ,  . Тогда уравнение высоты  имеет вид…
Варианты ответов: 1)  2) 
3)  4) 
Решение.
Вектор  перпендикулярен прямой PH. Тогда  .
Прямая PH проходит через точку  .
Тогда уравнение PH:  ;
 .
Ответ. №3
| | 2. Общее уравнение прямой
| Общее уравнение прямой
 ,
где  - координаты нормального вектора.
| Задача.
Найти нормальный вектор прямой  .
Решение.
Коэффициенты при переменных – это координаты нормального вектора.  .
| | 3. Уравнение прямой в отрезках
|  
Уравнение прямой в отрезках 
| | 4. Уравнение прямой с угловым коэффициентом
|
Уравнение прямой с угловым коэффициентом
 - угловой коэффициент, 
 - отрезок, отсекаемый прямой на оси  .
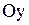| Задача.
Прямая проходит через точки  и  . Тогда ее угловой коэффициент равен…
Решение.
Уравнение прямой через две точки
 ;  .
Выразим y через x, тогда
 .
Следовательно, 
| | 5. Уравнение прямой, проходящей через точку с направляющим вектором
|
Уравнение прямой, проходящей через точку с направляющим вектором 
(направляющий вектор – вектор, параллельный прямой)
| Задача.
Написать уравнение прямой, проходящей через точки  параллельно вектору 
Решение.
| | 6. Уравнение прямой, проходящей через две точки
| 
Уравнение прямой, проходящей через две точки  и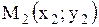 
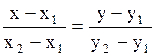
| Задача.
Написать уравнение прямой, проходящей через точки и .
Решение.
 .
Ответ. .
| | §3 Взаимное расположение прямых на плоскости
| | Вид уравнения прямой
| С угловым коэффициентом
| Общее уравнение
| С направляющим вектором
| | 15. Условие параллельности прямых
| 
| 
| 
| | 16. Условие перпендикулярности прямых
| 
| 
| 
| | 17. Угол между прямыми
| 
| 
| 
| Задача.
Уравнением прямой, перпендикулярной прямой  , является…
Варианты ответов: 1)  2)  3)  4) 
Решение.
Для прямой угловой коэффициент  , т.к. прямая должна быть перпендикулярной, то 
1) ,  ,  , 
2) ,  ,  ,
3) ,  , 
4) ,  , 
Ответ. №2.
Задача.
Среди прямых, заданных уравнениями  ,  ,  ,  , число неупорядоченных взаимно перпендикулярных пар прямых, равно…
Решение.
Для  ;
 ;
 ,  , ;
 ,  , .
 ;  ;  ;  , т.к.  .
Ответ. число неупорядоченных взаимно перпендикулярных пар прямых равно 4.
|
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Словарная работа в детском саду Словарная работа в детском саду — это планомерное расширение активного словаря детей за счет незнакомых или трудных слов, которое идет одновременно с ознакомлением с окружающей действительностью, воспитанием правильного отношения к окружающему...
Правила наложения мягкой бинтовой повязки 1. Во время наложения повязки больному (раненому) следует придать удобное положение: он должен удобно сидеть или лежать...
ТЕХНИКА ПОСЕВА, МЕТОДЫ ВЫДЕЛЕНИЯ ЧИСТЫХ КУЛЬТУР И КУЛЬТУРАЛЬНЫЕ СВОЙСТВА МИКРООРГАНИЗМОВ. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА БАКТЕРИЙ Цель занятия. Освоить технику посева микроорганизмов на плотные и жидкие питательные среды и методы выделения чистых бактериальных культур. Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения...
|
Неисправности автосцепки, с которыми запрещается постановка вагонов в поезд. Причины саморасцепов ЗАПРЕЩАЕТСЯ: постановка в поезда и следование в них вагонов, у которых автосцепное устройство имеет хотя бы одну из следующих неисправностей:
- трещину в корпусе автосцепки, излом деталей механизма...
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации...
|
|
, где 
- угол наклона прямой к положительному направлению оси 
.
, то 
.
и положительным направлением оси 
2) 
3) 
4) 
Решение.
Угол между прямой и положительным направлением оси 
, 
. Ответ. №1.
Задача.
Прямая образует с осью 
и проходит через точку 
. Написать ее уравнение.
Решение.
. Подставим k и координаты точки А в уравнение 
; 
.
2) 
3) 
4) 
Решение.
Сравнивая варианты ответов и вид параметрических уравнений, приходим к выводу
Ответ. №1.
до прямой 
2) 
3) 
Варианты ответов:
А) уравнение прямой с угловым коэффициентом
В) уравнение прямой, параллельной оси абсцисс
С) общее уравнение прямой
D) уравнение прямой, параллельной оси ординат
Е) уравнение прямой в отрезках на осях
Решение.
Проанализируем все уравнения
1. Уравнение вида 
. Это общее уравнение прямой.
2. Это уравнение вида 
. Это уравнение с угловым коэффициентом.
3. 
. Тогда прямая параллельна оси 
или 
)
или 
