Глава 10. Дифференциальное исчисление функции одной переменной
| 1 Формулы дифференцирования
| 1.  ;
2. ;
2.  ;
3. ;
3.  ;
4. ;
4. 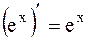 ;
5. ;
5.  ;
6. ;
6.  ; ;
| 7. 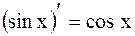 ;
8. ;
8. 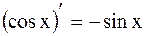 ;
9. ;
9.  ;
10. ;
10.  ;
11. ;
11. 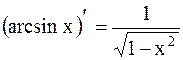 ;
12. ;
12.  ; ;
| 13.  14.
14. 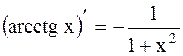 ;
15. ;
15. 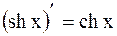 ;
16. ;
16. 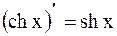 ;
17. ;
17. 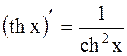 ;
18. ;
18. 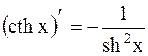 . .
| | 2 Основные правила дифференцирования
| Пусть функции  и и 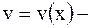 дифференцируемы в точке дифференцируемы в точке  . Тогда:
1. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: . Тогда:
1. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций:
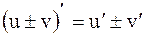 .
2. Производная произведения двух функций равна: .
2. Производная произведения двух функций равна:
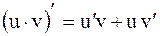 3. Производная частного двух функций равна:
3. Производная частного двух функций равна:
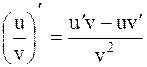 , если , если 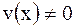 . .
| Задача.
Найти производные функций 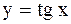 и и 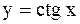 .
Решение.
Воспользуемся формулой производной частного: .
Решение.
Воспользуемся формулой производной частного:
  , т.е. , т.е. 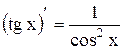 .
Аналогичным образом получим формулу .
Аналогичным образом получим формулу
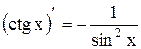 . .
| | 3 Производная сложной функции
| Пусть  и и  , тогда , тогда 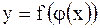 является сложной функцией переменной является сложной функцией переменной  , а переменную , а переменную  называют промежуточным аргументом.
Теорема.Если функция называют промежуточным аргументом.
Теорема.Если функция  имеет в некоторой точке имеет в некоторой точке  производную производную 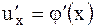 , а функция , а функция  имеет в соответствующей точке имеет в соответствующей точке  производную производную 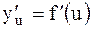 , то сложная функция , то сложная функция 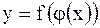 в указанной точке в указанной точке  также имеет производную, которая находится по формуле также имеет производную, которая находится по формуле
 или, коротко, или, коротко,

| Задача.
Найти производную функции  .
Решение.
Представим функцию как сложную, введя промежуточный аргумент .
Решение.
Представим функцию как сложную, введя промежуточный аргумент  : : 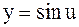 , где , где 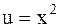 . Тогда . Тогда 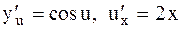 и, следовательно, и, следовательно,
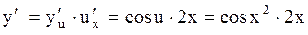 . .
| | 4 Производная обратной функции
| Теорема. Если функция  в некоторой точке в некоторой точке  имеет отличную от нуля производную имеет отличную от нуля производную  , то обратная ей функция , то обратная ей функция 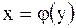 в соответствующей точке в соответствующей точке  также имеет
производную также имеет
производную 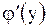 , равную , равную

| Задача.
Найти производную обратных тригонометрических функций  .
Решение.
Пусть .
Решение.
Пусть 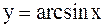 . Обратная ей функция имеет вид . Обратная ей функция имеет вид  , где , где  . В интервале . В интервале 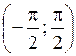 имеем имеем  . Тогда по правилу дифференцирования обратной функции . Тогда по правилу дифференцирования обратной функции
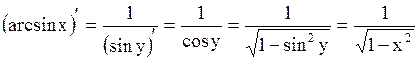 ,
где перед корнем взят знак +, так как ,
где перед корнем взят знак +, так как 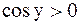 при при 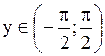 .
Итак, .
Итак, 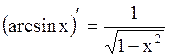 . .
| | 5 Производная неявно заданной функции
| Если функция задана неявным уравнением 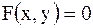 , т.е. не разрешенным относительно , т.е. не разрешенным относительно  , то для нахождения производной , то для нахождения производной  надо продифференцировать по надо продифференцировать по  обе части этого уравнения, учитывая, что обе части этого уравнения, учитывая, что  есть функция от есть функция от  , и затем разрешить полученное уравнение относительно , и затем разрешить полученное уравнение относительно  . .
| Задача.
Найти производную функции  , заданную уравнением , заданную уравнением 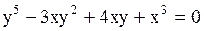 .
Решение.
Функция .
Решение.
Функция  задана неявно. Дифференцируя обе части этого тождества по задана неявно. Дифференцируя обе части этого тождества по  , считая, что , считая, что  есть функция от есть функция от  и, пользуясь правилом дифференцирования сложной функции, получим и, пользуясь правилом дифференцирования сложной функции, получим
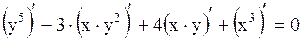
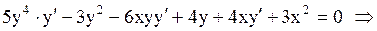
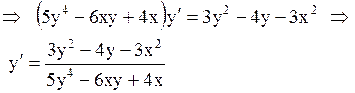
| | 6 Логарифмическое дифференцирование
| На практике встречаются функции, производные которых находят логарифмическим дифференцированием. К их числу относится так называемая степенно-показательная функция  .
Найдем производную, предварительно логарифмируя: .
Найдем производную, предварительно логарифмируя:
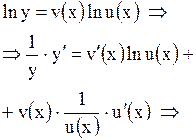
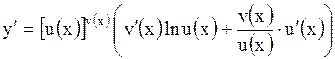 или или

| Задача.
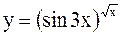 .
Решение.
Найдем логарифм данной функции .
Решение.
Найдем логарифм данной функции  или или  . Дифференцируя обе части этого равенства, получим . Дифференцируя обе части этого равенства, получим
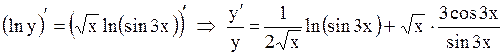 Отсюда
Отсюда 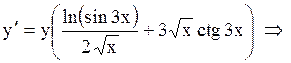
 Задача.
Задача.
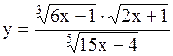 .
Решение.
Прологарифмируем данное равенство .
Решение.
Прологарифмируем данное равенство
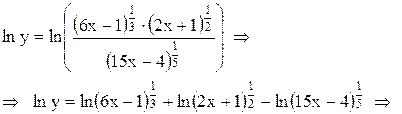
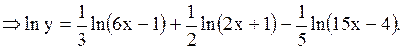 Дифференцируя обе части последнего равенства, получим
Дифференцируя обе части последнего равенства, получим
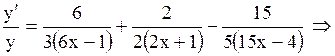
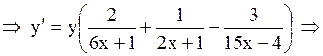
 . .
| | 7 Производная функции, заданной параметрически
| Если функция  аргумента аргумента  задана параметрическими уравнениями задана параметрическими уравнениями
 то производная функции
то производная функции  по переменной по переменной  , т.е. , т.е.  вычисляется по формуле: вычисляется по формуле:
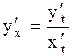 . .
| Задача.
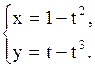 Решение.
Найдем
Решение.
Найдем 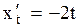 и и 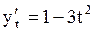 . Следовательно . Следовательно 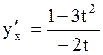 . .
| | 8 Касательная и нормаль к графику функции
| Уравнение прямой, касательной к графику  в точке в точке  имеет вид имеет вид
 .
Уравнение нормали, т.е. прямой, проходящей через точку .
Уравнение нормали, т.е. прямой, проходящей через точку 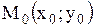 перпендикулярно к касательной, имеет вид перпендикулярно к касательной, имеет вид
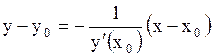 . .
| Задача.
Составить уравнение касательной и нормали к параболе  в точке в точке  .
Решение.
Найдем производную функции .
Решение.
Найдем производную функции  при при 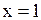 . Имеем . Имеем 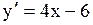 отсюда отсюда  .
В результате получим искомые уравнения касательной .
В результате получим искомые уравнения касательной 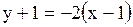 или или  и уравнение нормали и уравнение нормали  или или 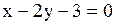 . .
| | 9 Дифференциал функции
| Дифференциал любой дифференцируемой функции  равен произведению ее производной на дифференциал независимой переменной. равен произведению ее производной на дифференциал независимой переменной.
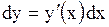
| Задача.
Найти дифференциал функции  .
Решение. .
Решение.
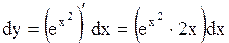 . .
| | 10 Приближенное вычисление с помощью дифференциала
| Если 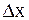 достаточно мало по абсолютной величине, то с точностью до бесконечно малых более высокого порядка малости, чем достаточно мало по абсолютной величине, то с точностью до бесконечно малых более высокого порядка малости, чем 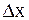 , имеет место приближенное равенство: , имеет место приближенное равенство:
 или или
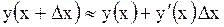 . .
| Задача.
Вычислить приближенное значение 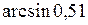 .
Решение.
Рассмотрим функцию .
Решение.
Рассмотрим функцию 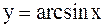 , полагая , полагая 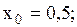  и применяя формулу и применяя формулу
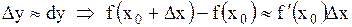  ,
получим ,
получим 

 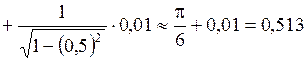 .
Ответ. 0,513. .
Ответ. 0,513.
| | 11 Производные высших порядков
| Производной  го порядка называют производную от производной го порядка называют производную от производной 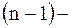 го порядка. Производную го порядка. Производную  го порядка обозначают го порядка обозначают  или или 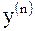
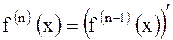 . .
| Задача.
Найти 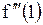 , если , если  .
Решение. .
Решение.
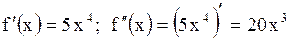 ; ;
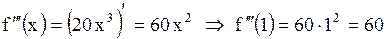 .
Ответ. 60. .
Ответ. 60.
| | 12 Производные высших порядков, заданных параметрически
| Если функция задана параметрически, то производные 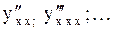 вычисляются по формулам вычисляются по формулам
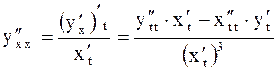

| Задача.
Найти  , если , если 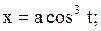 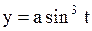 .
Решение. .
Решение.
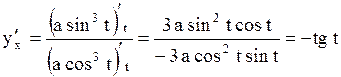
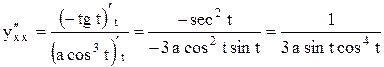 . .
| | 13 Дифференциалы высших порядков
| Дифференциалом  го порядканазывается дифференциал от дифференциала го порядканазывается дифференциал от дифференциала 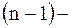 го порядка: го порядка:
 или
или
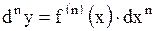
| Задача.
Найти дифференциалы второго и третьего порядков функции 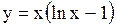 .
Решение. .
Решение.
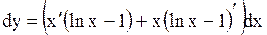 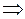 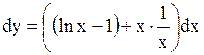 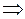
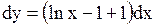 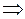  . .
 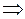 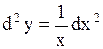 ; ;
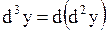 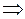 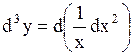 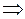 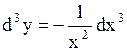 . .
| | 14 Правило Лопиталя
| Пусть функции  и и 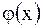 дифференцируемы в дифференцируемы в  окрестности точки окрестности точки  и и 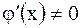 при всех при всех  из этой окрестности, тогда, если из этой окрестности, тогда, если
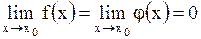 или
или
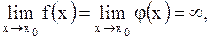 т.е. частное
т.е. частное  имеет в точке имеет в точке 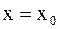 неопределенность типа неопределенность типа  или или  , то , то
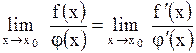 при условии, что существует предел отношения производных.
Правило Лопиталя применяется для раскрытия неопределенностей вида
при условии, что существует предел отношения производных.
Правило Лопиталя применяется для раскрытия неопределенностей вида  и и  . Но на практике встречаются неопределенности вида . Но на практике встречаются неопределенности вида  , ,  . Эти неопределенности путем элементарных преобразований можно свести к неопределенностям вида . Эти неопределенности путем элементарных преобразований можно свести к неопределенностям вида  или или  . .
| Задача.
Найти 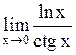 .
Решение.
Здесь имеет место неопределенность .
Решение.
Здесь имеет место неопределенность  . Применим правило Лопиталя, т.е. рассмотрим предел отношения производных заданных функций . Применим правило Лопиталя, т.е. рассмотрим предел отношения производных заданных функций
 .
Последний предел дает неопределенность .
Последний предел дает неопределенность 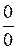 . Снова применим правило Лопиталя и получим . Снова применим правило Лопиталя и получим
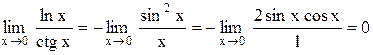 .
Задача.
Найти .
Задача.
Найти  Решение.
Решение.
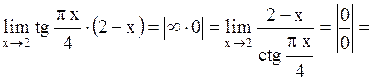 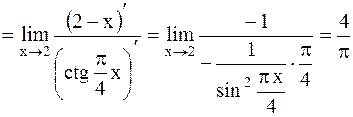 .
Задача.
Найти .
Задача.
Найти  Решение.
Решение.
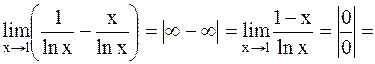
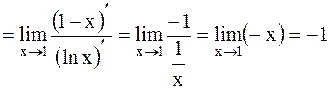 . .
| | | | | | | | | |
| 15 Теорема Ролля
| Теорема (Ролля).Пусть функция  удовлетворяет следующим условиям:
1. непрерывна на отрезке удовлетворяет следующим условиям:
1. непрерывна на отрезке  ,
2. дифференцируема в интервале ,
2. дифференцируема в интервале  ,
3. на концах отрезка принимает одинаковые значения: ,
3. на концах отрезка принимает одинаковые значения:  .
Тогда внутри отрезка .
Тогда внутри отрезка 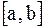 найдется хотя бы одна точка найдется хотя бы одна точка 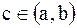 , в которой производная , в которой производная  обращается в нуль, т.е. обращается в нуль, т.е.  .
Геометрически теорема Ролля означает, что на графике функции .
Геометрически теорема Ролля означает, что на графике функции  найдется хотя бы одна точка, в которой касательная к графику параллельна оси найдется хотя бы одна точка, в которой касательная к графику параллельна оси 

| Задача.
Выполняется ли теорема Ролля для функции 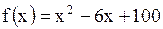 , если , если  , , 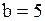 ? При каком значении ? При каком значении 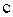 ?
Решение.
Так как функция ?
Решение.
Так как функция  непрерывна и дифференцируема при всех значениях непрерывна и дифференцируема при всех значениях  и ее значения на концах отрезка и ее значения на концах отрезка 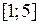 равны: равны:
 . .
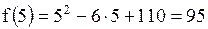 , то теорема Ролля на этом отрезке выполняется. Значит с определяется из уравнения , то теорема Ролля на этом отрезке выполняется. Значит с определяется из уравнения
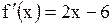 ; ;
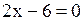 ; ;
 .
Следовательно, .
Следовательно, 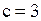 Ответ. выполняется,
Ответ. выполняется, 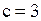 . .
| | 16 Теорема Лагранжа
| Теорема (Лагранжа). Если функция  1. непрерывна на отрезке
1. непрерывна на отрезке 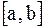 ,
2. дифференцируема в интервале ,
2. дифференцируема в интервале  , то найдется хотя бы одна точка , то найдется хотя бы одна точка 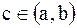 такая, что такая, что

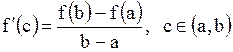 .
Теорема Лагранжа имеет простой геометрический смысл. Отношение .
Теорема Лагранжа имеет простой геометрический смысл. Отношение 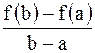 есть угловой коэффициент секущей есть угловой коэффициент секущей 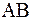 , а , а 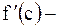 угловой коэффициент касательной к кривой в точке с абсциссой угловой коэффициент касательной к кривой в точке с абсциссой 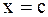 . .
| Задача. Проверить справедливость теоремы Лагранжа для функции  на отрезке на отрезке  .
Решение.
Функция определена при всех значениях .
Решение.
Функция определена при всех значениях 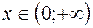 , а следовательно и на отрезке , а следовательно и на отрезке  . Функция дифференцируема на интервале . Функция дифференцируема на интервале  .
Найдем точку с, для которой выполняется равенство .
Найдем точку с, для которой выполняется равенство 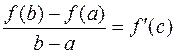 , где , где 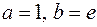 . .
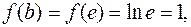 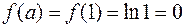 , ,
  , ,
 . Откуда . Откуда  , причем , причем  . .
| | 17 Теорема Коши
| Теорема (Коши). Если функции  и и 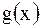 1. непрерывны на отрезке
1. непрерывны на отрезке 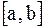 ,
2. дифференцируемы в интервале ,
2. дифференцируемы в интервале  , причем , причем  для всех для всех  , то найдется хотя бы одна точка , то найдется хотя бы одна точка 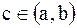 такая, что такая, что
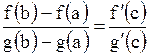
| | 18 Теорема Ферма
| Теорема (Ферма). Пусть функция  определена на интервале определена на интервале 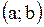 и в некоторой точке и в некоторой точке 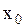 этого интервала принимает наибольшее или наименьшее значение. Тогда, если в точке этого интервала принимает наибольшее или наименьшее значение. Тогда, если в точке 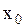 существует производная, то она равна 0, то есть существует производная, то она равна 0, то есть 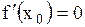 . .
| | 19 Интервалы монотонности
| Теорема (достаточные условия). Если функция  дифференцируема в интервале дифференцируема в интервале  и и 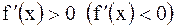 для для  , то эта функция возрастает (убывает) в интервале , то эта функция возрастает (убывает) в интервале  . .
| Задача.
Определить интервалы монотонности функции  .
Решение. Найдем .
Решение. Найдем  . Функция возрастает для всех значений . Функция возрастает для всех значений  , для которых , для которых 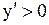 . Решая неравенство . Решая неравенство  , получим , получим  .
Аналогично, решая неравенство .
Аналогично, решая неравенство  , получим , получим  .
Следовательно, функция возрастает в промежутках .
Следовательно, функция возрастает в промежутках 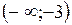 и и 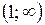 и убывает в интервале и убывает в интервале 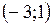 . .
| | 20 Экстремум функции
| Точки, в которых производная  равна нулю или не существует, называются критическими точками функции. Если дифференцируемая функция y=f(x) в точке равна нулю или не существует, называются критическими точками функции. Если дифференцируемая функция y=f(x) в точке  имеет экстремум, то ее производная в этой точке равна нулю, то есть имеет экстремум, то ее производная в этой точке равна нулю, то есть 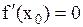 (необходимое условие экстремума функции) (необходимое условие экстремума функции)
 Теорема (достаточное условие экстремума). Теорема (достаточное условие экстремума).
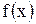 непрерывна в некотором интервале содержащем критическую точку непрерывна в некотором интервале содержащем критическую точку  . Если функция . Если функция  дифференцируема в некоторой окрестности критической точки дифференцируема в некоторой окрестности критической точки  (кроме, быть может, самой точки (кроме, быть может, самой точки  ) и при переходе аргумента ) и при переходе аргумента  через нее слева направо производная через нее слева направо производная  меняет знак с плюса на минус, то меняет знак с плюса на минус, то 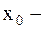 точка максимума; если точка максимума; если  меняет знак с минуса на плюс, то меняет знак с минуса на плюс, то 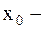 точка минимума. точка минимума.
| Задача.
Найти экстремумы функции 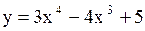 .
Решение.
Очевидно, что .
Решение.
Очевидно, что 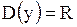 . Находим . Находим  . Определим критические точки: . Определим критические точки: 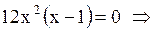 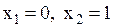 . Эти критические точки разбивают всю область определения функции на интервалы . Эти критические точки разбивают всю область определения функции на интервалы 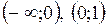 и и 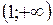 . Полученные результаты удобно представить в виде следующей таблицы: . Полученные результаты удобно представить в виде следующей таблицы:
Из таблицы видно, что в точке  нет экстремума, а нет экстремума, а  точка минимума. Минимум этой функции равен точка минимума. Минимум этой функции равен  . .
| | | | | | |
| 21 Нахождение наибольшего и наименьшего значения функции
| Для нахождения наибольшего и наименьшего значений функции на отрезке 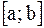 необходимо:
1. найти критические точки на необходимо:
1. найти критические точки на  ;
2. вычислить значения функции в найденных критических точках и в точках ;
2. вычислить значения функции в найденных критических точках и в точках  , , 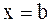 ;
3. из этих значений выбрать наибольшее и наименьшее. ;
3. из этих значений выбрать наибольшее и наименьшее.
| Задача.
Найти наибольшее и наименьшее значения функции 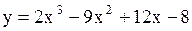 на на 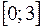 Решение.
Находим критические точки:
Решение.
Находим критические точки:
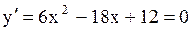 , , 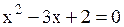 , , 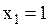 , , 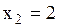 , , 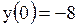 , , 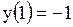 , ,  , , 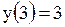 .
Наибольшее значение функции при .
Наибольшее значение функции при  равно 3.
Наименьшее значение функции при равно 3.
Наименьшее значение функции при 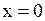 равно -8. равно -8.
| | 22 Вертикальная асимптота
| Прямая  называется вертикальной асимптотой графикафункции называется вертикальной асимптотой графикафункции  , если хотя бы один из односторонних пределов функции в этой точке равен бесконечности, то есть , если хотя бы один из односторонних пределов функции в этой точке равен бесконечности, то есть 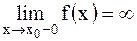 или или  . .
| Задача.
Кривая  имеет вертикальную асимптоту имеет вертикальную асимптоту  , так как , так как  и и 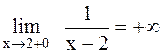 . .
| | 23 Горизонтальная асимптота
| Прямая 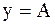 называется горизонтальной асимптотой графикафункции называется горизонтальной асимптотой графикафункции  при при  (или (или  ), если ), если  . .
| Задача.
Прямая 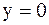 является горизонтальной асимптотой кривой является горизонтальной асимптотой кривой  , так как , так как 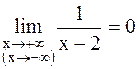 . .
| | 24 Наклонная асимптота
| Прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.
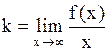 ; ; 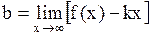
| Задача.
Найти асимптоты и построить график функции 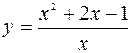 .
1) Вертикальные асимптоты: y®+¥ x®0-0: y®-¥ x®0+0, следовательно, х = 0- вертикальная асимптота.
2) Наклонные асимптоты: .
1) Вертикальные асимптоты: y®+¥ x®0-0: y®-¥ x®0+0, следовательно, х = 0- вертикальная асимптота.
2) Наклонные асимптоты:

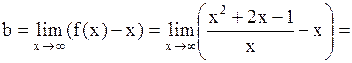
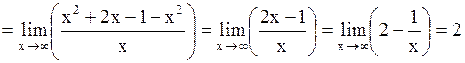 Таким образом, прямая у = х + 2 является наклонной асимптотой.
Построим график функции:
Таким образом, прямая у = х + 2 является наклонной асимптотой.
Построим график функции:

| | 25 Мера плоского множества
| | Мера множества, математическое понятие, обобщающее понятия длины отрезка, площади плоской фигуры и объёма тела на множества более общей природы. В качестве примера можно привести определение меры Лебега (введённой А. Лебегом в 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения.
| Задача.
Мера множества, изображенного на рисунке, 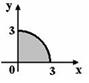 равна…
Решение.
Мерой данного множества будет площадь четверти круга, следовательно, если площадь круга равна…
Решение.
Мерой данного множества будет площадь четверти круга, следовательно, если площадь круга  , то площадь четверти круга , то площадь четверти круга  .
Ответ. .
Ответ.  .
Задача.
Мера плоского множества, изображенного на рисунке, .
Задача.
Мера плоского множества, изображенного на рисунке,
 равна…
Решение.
Площадь заштрихованного треугольника и будет мера данного множества, следовательно, используя геометрический смысл определенного интеграла для нахождения площади, получим:
равна…
Решение.
Площадь заштрихованного треугольника и будет мера данного множества, следовательно, используя геометрический смысл определенного интеграла для нахождения площади, получим: 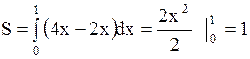 .
Ответ. 1 .
Ответ. 1
| | | | | | |

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Дизартрии у детей Выделение клинических форм дизартрии у детей является в большой степени условным, так как у них крайне редко бывают локальные поражения мозга, с которыми связаны четко определенные синдромы двигательных нарушений...
Педагогическая структура процесса социализации Характеризуя социализацию как педагогический процессе, следует рассмотреть ее основные компоненты: цель, содержание, средства, функции субъекта и объекта...
Типовые ситуационные задачи. Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической
Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической нагрузке. Из медицинской книжки установлено, что он страдает врожденным пороком сердца....
|
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит...
Кран машиниста усл. № 394 – назначение и устройство Кран машиниста условный номер 394 предназначен для управления тормозами поезда...
Приложение Г: Особенности заполнение справки формы ву-45
После выполнения полного опробования тормозов, а так же после сокращенного, если предварительно на станции было произведено полное опробование тормозов состава от стационарной установки с автоматической регистрацией параметров или без...
|
|