1. Решение. Нет, поскольку не выполняется первая аксиома. Если  , то
, то  , т.е.
, т.е. 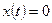 на отрезке
на отрезке  . Но, вообще говоря,
. Но, вообще говоря,  на всем отрезке
на всем отрезке  .
.
2. Решение. Нет, не выполняется первая аксиома. Если  , то
, то 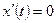 на отрезке
на отрезке  . Поэтому
. Поэтому 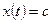 , которая может не обращаться в нуль.
, которая может не обращаться в нуль.
3. Решение. Да. В этом случае постоянная, которая появляется, как и в предыдущей задаче должна обращаться в нуль. Нетрудно доказываются другие аксиомы.
4. Решение. Нет, поскольку не выполняется вторая аксиома. В силу второй аксиомы нормы для любых вещественных чисел  и
и  должно выполняться соотношение
должно выполняться соотношение
 .
.
Положив здесь  ,
, 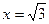 , получаем
, получаем  , что неверно.
, что неверно.
5. Решение. Первые две аксиомы проверяются без труда. Проверим аксиому треугольника. Имеем

 . Так как это неравенство справедливо при всех
. Так как это неравенство справедливо при всех 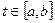 , то получим
, то получим

 .
.
Суммируя это неравенство, когда  пробегает от 0 до
пробегает от 0 до  , получим неравенство треугольника.
, получим неравенство треугольника.
6. Решение. По условию существует ненулевой элемент, т.е. такой элемент  , что
, что  . Пусть
. Пусть  - произвольное неотрицательное число. Положим
- произвольное неотрицательное число. Положим  , тогда
, тогда  . Утверждение доказано.
. Утверждение доказано.
7. Решение. Согласно задачи 6, существует такой элемент  , что
, что 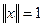 . Тогда элемент
. Тогда элемент  лежит на сфере.
лежит на сфере.
8. Решение. Для любых  имеем
имеем
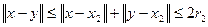 .
.
Далее в шаре 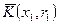 есть такая точка
есть такая точка 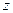 , что
, что  . Точка
. Точка 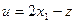 также лежит в указанном шаре, причем
также лежит в указанном шаре, причем
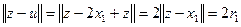 .
.
Если бы мы имели  и
и  , то с одной стороны
, то с одной стороны  , а с другой стороны
, а с другой стороны  , так как
, так как  . Полученное противоречие и доказывает утверждение задачи.
. Полученное противоречие и доказывает утверждение задачи.
9. Доказательство. Пусть  , т.е.
, т.е. 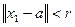 ,
,  . Возьмем произвольный элемент вида
. Возьмем произвольный элемент вида  ,
,  . Имеем
. Имеем
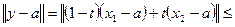
 .
.
Итак  , и, следовательно,
, и, следовательно, 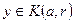 .
.
10. Доказательство. Пусть  и
и  . Рассмотрим произвольный шар
. Рассмотрим произвольный шар  . Точки вид
. Точки вид  попадают в шар
попадают в шар  при больших
при больших  . Но
. Но 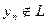 , в противном случае и точка
, в противном случае и точка  принадлежала бы линейному многообразию
принадлежала бы линейному многообразию  . Следовательно, никакой шар не может принадлежать данному многообразию
. Следовательно, никакой шар не может принадлежать данному многообразию  .
.
11. Доказательство. Пусть в бесконечномерном банаховом пространстве  существует счетный алгебраический базис
существует счетный алгебраический базис  . Это означает, что каждый элемент представляется в виде конечной суммы
. Это означает, что каждый элемент представляется в виде конечной суммы
 ,
,
причем  зависит от элемента
зависит от элемента  . Рассмотрим последовательность конечномерных подпространств
. Рассмотрим последовательность конечномерных подпространств
 .
.
В силу предложения 18 второй главы, линейное многообразие  замкнуто и по определению алгебраического базиса
замкнуто и по определению алгебраического базиса
 .
.
По теореме Бэра хотя бы одно из подпространств  имеет внутреннюю точку, а согласно задачи 10 линейное многообразие, отличное от всего пространства не имеет внутренних точек. Полученное противоречие доказывает утверждение.
имеет внутреннюю точку, а согласно задачи 10 линейное многообразие, отличное от всего пространства не имеет внутренних точек. Полученное противоречие доказывает утверждение.
12. Доказательство. Рассмотрим случай, когда 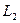 имеет размерность один, далее утверждение доказывается методом математической индукции
имеет размерность один, далее утверждение доказывается методом математической индукции
Обозначим через  линейное многообразие, порожденное подпространством
линейное многообразие, порожденное подпространством  и вектором
и вектором  . Требуется доказать замкнутость
. Требуется доказать замкнутость  . Если
. Если
 , то
, то  и поэтому замкнуто. Пусть теперь
и поэтому замкнуто. Пусть теперь  . Согласно предложения 19 из второй главы,
. Согласно предложения 19 из второй главы,  . Линейное многообразие
. Линейное многообразие  состоит из векторов вида
состоит из векторов вида  , где
, где  . Докажем, что
. Докажем, что
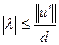 . (5.1)
. (5.1)
Имеем  , если
, если  , если же
, если же 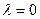 , то неравенство (5.1) очевидно.
, то неравенство (5.1) очевидно.
Далее пусть 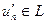 и
и 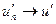 , когда
, когда 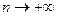 ; требуется доказать, что
; требуется доказать, что  . Пусть
. Пусть  ,
,  . Применяя неравенство (6.1) к вектору
. Применяя неравенство (6.1) к вектору  , получим
, получим
 ,
, 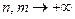 .
.
Поэтому  стремится к некоторому пределу
стремится к некоторому пределу  и
и
 .
.
Поскольку  замкнуто и
замкнуто и  , то
, то  . Итак,
. Итак,  , что и требовалось доказать.
, что и требовалось доказать.
13. Решение. а) Нет. Согласно теоремы Вейерштрасса, линейное многообразие многочленов всюду плотно в пространстве  . И поскольку в этом пространстве имеются другие функции, помимо многочленов, то линейное многообразие многочленов не является замкнутым;
. И поскольку в этом пространстве имеются другие функции, помимо многочленов, то линейное многообразие многочленов не является замкнутым;
б) Да. Линейное многообразие многочленов степени меньше или равно фиксированного  является конечномерным и поэтому замкнутым;
является конечномерным и поэтому замкнутым;
в) Да. Сходимость в пространстве  означает равномерную сходимость, из которой следует сходимость в каждой точке. Поэтому, если последовательность
означает равномерную сходимость, из которой следует сходимость в каждой точке. Поэтому, если последовательность  сходится к
сходится к  и каждый элемент последовательности удовлетворяет условию
и каждый элемент последовательности удовлетворяет условию 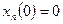 , то и предельная функция удовлетворяет этому же условию, те.
, то и предельная функция удовлетворяет этому же условию, те. 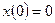 .
.
г) Да. Сходимость в  или равномерная сходимость обеспечивает сходимость соответствующих интегралов. Поэтому, если
или равномерная сходимость обеспечивает сходимость соответствующих интегралов. Поэтому, если  для каждого элемента последовательности, то и для предельного элемента справедливо равенство:
для каждого элемента последовательности, то и для предельного элемента справедливо равенство:  .
.
14. Доказательство. Пусть последовательность

и  при
при 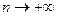 в
в 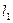 . Это означает, что для любого
. Это означает, что для любого  существует
существует  такое, что для всех
такое, что для всех  справедливо неравенство
справедливо неравенство
 .
.
Отсюда следует
 .
.
При выводе последнего неравенства использовали то, что  . И поскольку
. И поскольку  произвольно, то
произвольно, то 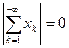 , т.е.
, т.е. 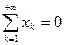 . Следовательно,
. Следовательно,  - подпространство в
- подпространство в 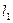 .
.
15. Доказательство. Рассмотрим последовательность вида
 .
.
Здесь ровно  координат элемента
координат элемента  , начиная со второго, равны числу
, начиная со второго, равны числу 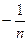 .
.
Покажем, что  . В самом деле
. В самом деле
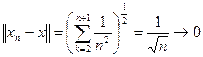 при
при 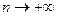 .
.
Но  . Следовательно, линейное многообразие
. Следовательно, линейное многообразие  не является подпространством в
не является подпространством в  . Утверждение доказано.
. Утверждение доказано.
16. Доказательство. Пусть последовательность
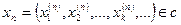
и  при
при 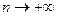 в
в  . Для любого
. Для любого  найдется
найдется  такое, что для всех
такое, что для всех  справедливо неравенство
справедливо неравенство
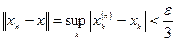
или
 ,
,  .
.
Зафиксируем  . Поскольку
. Поскольку  , то последовательность
, то последовательность  сходится. Поэтому существует
сходится. Поэтому существует  такое, что для всех
такое, что для всех  будет
будет
 .
.
С учетом полученных оценок для  найдем
найдем
 .
.
Отсюда следует, что последовательность  является сходящейся. Утверждение доказано.
является сходящейся. Утверждение доказано.
17.Доказательство. Пункт a) доказывается так же, как и в задаче
13. Далее обозначим через 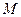 одномерное подпространство, порожденное постоянной функцией
одномерное подпространство, порожденное постоянной функцией  . Легко увидеть, что
. Легко увидеть, что 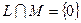 . Произвольную
. Произвольную  функцию из пространства
функцию из пространства 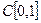 представим в виде
представим в виде
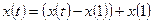 .
.
Здесь первое слагаемое принадлежит подпространству  , в второе – подпространству
, в второе – подпространству 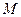 . Для завершения доказательства остается применить предложение 7 из первой главы.
. Для завершения доказательства остается применить предложение 7 из первой главы.
18. Решение. Пусть  - множество четных непрерывных на отрезке
- множество четных непрерывных на отрезке  функций. Очевидно,
функций. Очевидно,  образует линейное многообразие в
образует линейное многообразие в  . Докажем замкнутость. Возьмем последовательность четных функций
. Докажем замкнутость. Возьмем последовательность четных функций  , которая сходится к функции
, которая сходится к функции  в пространстве
в пространстве  . Тогда
. Тогда
 ,
,
откуда следует, что 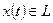 . Аналогично доказывается, что множество
. Аналогично доказывается, что множество 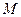 всех нечетных непрерывных функций образует подпространство. Далее каждая функция представляется в виде четной и нечетной функций. Учитывая соотношение
всех нечетных непрерывных функций образует подпространство. Далее каждая функция представляется в виде четной и нечетной функций. Учитывая соотношение 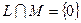 и применяя предложение 7 из первой главы, получим полное решение задачи.
и применяя предложение 7 из первой главы, получим полное решение задачи.
19. Решение. Нет. Для доказательства в пространстве  рассмотрим множество
рассмотрим множество  , элементами которого являются последовательности вида
, элементами которого являются последовательности вида
 .
.
Здесь перед ненулевым числом имеется ровно  нулей. Легко увидеть, что
нулей. Легко увидеть, что  , если
, если  дл. Следовательно, каждая точка множества
дл. Следовательно, каждая точка множества  является изолированной и поэтому множество
является изолированной и поэтому множество  - замкнуто. Далее возьмем
- замкнуто. Далее возьмем  . Тогда
. Тогда  , но ни при каком
, но ни при каком  , очевидно,
, очевидно, 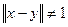
Задача решена.
20. Доказательство. Очевидно, 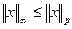 . Далее из определения нормы следует, что
. Далее из определения нормы следует, что  ,
,  . Отсюда
. Отсюда
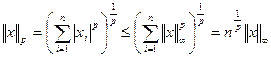 .
.
Тем самым доказана эквивалентность норм.
21. Да. Очевидно, 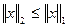 . Представим произвольную функцию
. Представим произвольную функцию  в виде
в виде
 .
.
Отсюда следует неравенство
 ,
,  .
.
Из этого неравенства и определения норм получаем

и эквивалентность двух норм установлена.
22. Доказательство. Положим  . Тогда из неравенств
. Тогда из неравенств
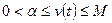
нетрудно получаются неравенства
 ,
,
которые и означает эквивалентность двух норм.
23. Доказательство. Согласно предложения 14 из второй главы, две нормы эквивалентны тогда и только тогда, когда из сходимости по одной норме вытекает ее сходимость по другой норме и наоборот.
Введем в рассмотрение последовательность  ,
,  . Тогда
. Тогда
 , при
, при 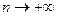 .
.
Покажем, что последовательность не сходится по другой норме. Для этого достаточно доказать, что она не является фундаментальной. Имеем
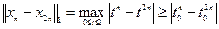 .
.
Взяв 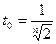 , получим отсюда, что
, получим отсюда, что
 .
.
Полученное неравенство и означает, что последовательность не является фундаментальной. Утверждение доказано.
24. Да. То, что норма  подчинена норме
подчинена норме 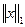 , проверяется непосредственно:
, проверяется непосредственно:
 .
.
А для доказательства того, что 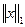 подчинена норме
подчинена норме  нам потребуется вспомогательное тождество.
нам потребуется вспомогательное тождество.
Для произвольного фиксированного  имеем
имеем
 . (5.2)
. (5.2)
Интегрируя равенство (6.1) по  в пределах от
в пределах от  до 1 и изменяя порядок интегрирования в двойном интеграле, получим
до 1 и изменяя порядок интегрирования в двойном интеграле, получим
 . (5.3)
. (5.3)
Аналогично, проинтегрировав (5.2) по  в пределах от 0 до
в пределах от 0 до  и просуммировав результат с (5.3), получим
и просуммировав результат с (5.3), получим
 , (5.4)
, (5.4)
где функция  ограничена в квадрате
ограничена в квадрате  .
.
С помощью тождества (5.4) уже непосредственно выводится неравенство
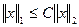
Задача полностью решена.
25. Доказательство. Согласно предложения 3 второй главы, метрика,
порожденная нормой, должна обладать свойством положительной однородности:  . Покажем, что это свойство в нашем случае не выполняется. Взяв
. Покажем, что это свойство в нашем случае не выполняется. Взяв  , найдем
, найдем  ,
,  . Следовательно,
. Следовательно,
 .
.
Утверждение доказано.
26. Доказательство. Докажем от противного. Предположим, что можно
ввести норму. Рассмотрим последовательность ненулевых элементов  , где
, где  ,
,  ,…,
,…,  ,…. Поскольку элементы ненулевые, то
,…. Поскольку элементы ненулевые, то  . Положим
. Положим 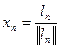 . Согласно второй аксиомы для нормы
. Согласно второй аксиомы для нормы  .
.
Далее оценим расстояние между  и 0:
и 0:
 ,когда
,когда 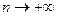 .
.
Следовательно, в метрическом пространстве последовательность  стремится к нулю. Но норма
стремится к нулю. Но норма  , эта же последовательность не стремится к нулю по норме. Утверждение доказано.
, эта же последовательность не стремится к нулю по норме. Утверждение доказано.
27. Рассмотрим последовательность  многочленов, где
многочленов, где
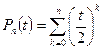 .
.
Нетрудно показать, что данная последовательность является фундаментальной по каждой из норм, но не имеет предела в линейном многообразии многочленов.
Второй способ доказательства. В силу задачи 11, в бесконечномерном банаховом пространстве не может существовать счетного алгебраического базиса. Пространство многочленов по определению имеет счетный базис и поэтому не может быть полным относительно какой-нибудь нормы.
28. Пусть  - фундаментальная последовательность в пространстве
- фундаментальная последовательность в пространстве  . Тогда для произвольного положительного
. Тогда для произвольного положительного  найдется такой номер
найдется такой номер  , что при
, что при 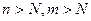
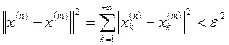 . (5.5)
. (5.5)
Поскольку при каждом фиксированном 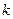
 ,
,
то числовая последовательность  - фундаментальна и, следовательно, сходится к некоторому пределу
- фундаментальна и, следовательно, сходится к некоторому пределу  :
:
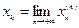 .
.
Составим вектор  . Далее из (5.5) для любого натурального
. Далее из (5.5) для любого натурального  имеем
имеем
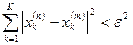 .
.
Устремляя в этом неравенстве  к бесконечности, получаем
к бесконечности, получаем
 . (5.6)
. (5.6)
Поскольку это неравенство справедливо для любого  , то
, то
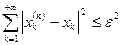 . (5.7)
. (5.7)
Из сходимости рядов  и
и  вытекает сходимость ряда
вытекает сходимость ряда  .
.
И поскольку  произвольно, то неравенство (5.7) означает, что
произвольно, то неравенство (5.7) означает, что
 .
.
Полнота пространства полностью доказана.
29. Пусть  - фундаментальная последовательность в пространстве
- фундаментальная последовательность в пространстве  . Это означает, что для произвольного положительного
. Это означает, что для произвольного положительного  найдется такой номер
найдется такой номер  , что при
, что при 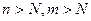
 . (5.8)
. (5.8)
Отсюда следует, что
 (5.9)
(5.9)
при любом 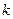 и
и 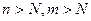 .
.
Последнее неравенство означает, что числовая последовательность  - фундаментальна и, следовательно, сходится к некоторому пределу
- фундаментальна и, следовательно, сходится к некоторому пределу  . А теперь в неравенстве (5.9) устремляя
. А теперь в неравенстве (5.9) устремляя  к бесконечности, получим
к бесконечности, получим
 . (5.10)
. (5.10)
Отсюда
 .
.
Из этого неравенства и ограниченности последовательности  следует ограниченность последовательности
следует ограниченность последовательности  . Нам остается доказать, что последовательность
. Нам остается доказать, что последовательность  сходится к элементу
сходится к элементу  по норме пространства
по норме пространства  .
.
Из неравенства (5.10), справедливого при любом 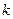 , вытекает,
, вытекает,
что
 при
при  .
.
А так как  произвольно, то
произвольно, то
 при
при 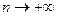
и полнота пространства  доказана.
доказана.
30. Пусть  - фундаментальная последовательность в пространстве
- фундаментальная последовательность в пространстве  . Выберем подпоследовательность
. Выберем подпоследовательность  так, чтобы
так, чтобы
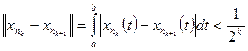
и рассмотрим ряд
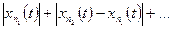 (5.11)
(5.11)
Члены этого ряда неотрицательны и интегралы от его частичных сумм не превосходят  . По теореме Леви из теории интеграла Лебега [2,3] ряд (5.11) сходится почти всюду на отрезке
. По теореме Леви из теории интеграла Лебега [2,3] ряд (5.11) сходится почти всюду на отрезке  . Поскольку абсолютно сходящийся числовой ряд сходится, то также и ряд
. Поскольку абсолютно сходящийся числовой ряд сходится, то также и ряд
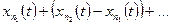
сходится почти всюду к некоторой функции
 .
.
Покажем теперь, что подпоследовательность  сходится к той же функции
сходится к той же функции  по норме. В силу фундаментальности последовательности
по норме. В силу фундаментальности последовательности  при любом фиксированном
при любом фиксированном  для достаточно больших
для достаточно больших 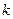 и
и 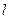 имеем
имеем
 .
.
Согласно теореме Фату также из теории интеграла Лебега в этом интеграле можно перейти к пределу, когда  . В результате получаем
. В результате получаем
 ,
,
откуда следует, что  и
и  по норме. А из того, что фундаментальная последовательность содержит подпоследовательность, сходящуюся к некоторому пределу, следует, что и сама последовательность сходится к тому же пределу.
по норме. А из того, что фундаментальная последовательность содержит подпоследовательность, сходящуюся к некоторому пределу, следует, что и сама последовательность сходится к тому же пределу.
Теорем полностью доказана.
31. Доказательство. Ввиду неполноты пространства существует фундаментальная последовательность  , не имеющего предела.
, не имеющего предела.
Выберем подпоследовательность  так, чтобы
так, чтобы
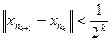
и рассмотрим ряд
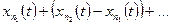 . (5.12)
. (5.12)
Этот ряд абсолютно сходится, поскольку
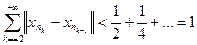 .
.
В то же время частичные суммы ряда (5.12) равны  и поэтому образуют расходящуюся последовательность. Утверждение доказано.
и поэтому образуют расходящуюся последовательность. Утверждение доказано.
32. Доказательство. Пусть 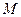 замкнуто. Всякая фундаментальная последовательность элементов из
замкнуто. Всякая фундаментальная последовательность элементов из 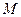 сходится, в силу полноты
сходится, в силу полноты  , к некоторому элементу
, к некоторому элементу  . И поскольку
. И поскольку 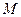 замкнуто, то
замкнуто, то  .
.
Обратно, пусть 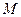 полно и
полно и  является предельной точкой множества
является предельной точкой множества 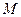 . Тогда существует последовательность
. Тогда существует последовательность  , сходящаяся к
, сходящаяся к  . Но
. Но  - фундаментальная последовательность и, в виду полноты
- фундаментальная последовательность и, в виду полноты 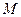 , сходится к элементу
, сходится к элементу  из множества
из множества 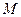 . А из единственности предела следует, что
. А из единственности предела следует, что  и, следовательно,
и, следовательно,  принадлежит множеству
принадлежит множеству 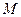 . Утверждение доказано.
. Утверждение доказано.
33. Доказательство. Если  при
при 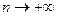 , то шары имеют общую точку по теореме 3 из третьей главы. В противном случае или
, то шары имеют общую точку по теореме 3 из третьей главы. В противном случае или  стабилизируются и тогда соответственно шары совпадают ил же, наконец,
стабилизируются и тогда соответственно шары совпадают ил же, наконец, 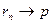 ,
,  . В последнем случае последовательность шаров с теми же центрами, радиусы которых равны
. В последнем случае последовательность шаров с теми же центрами, радиусы которых равны 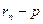 , является вложенной и по доказанному имеет непустое пересечение. Утверждение доказано.
, является вложенной и по доказанному имеет непустое пересечение. Утверждение доказано.
34. Для доказательства приведем примеры. Пример 1. Пусть  ,
,  ,…,
,…,  ,… Положив
,… Положив
 ,
,
получим требуемую последовательность.
Пример 2. В пространстве 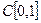 рассмотрим множества
рассмотрим множества
 .
.
Нетрудно показать, что в обоих примерах введенные множества удовлетворяют условиям утверждения. Утверждение доказано.
35. Доказательство. Пусть функции  и
и  принадлежат одному классу смежности
принадлежат одному классу смежности  . Тогда
. Тогда 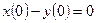 или
или  . Взяв в каждом классе смежности по представителю
. Взяв в каждом классе смежности по представителю 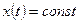 , получим взаимно однозначное соответствие между множеством действительных чисел
, получим взаимно однозначное соответствие между множеством действительных чисел  и фактор-пространством
и фактор-пространством  . Указанное соответствие является изоморфизмом.
. Указанное соответствие является изоморфизмом.
ЛИТЕРАТУРА
1. Шилов Г.Е. Введение в теорию линейных пространств. М.-Л.: Гос. изд-во технико-теоретической литературы, 1952. 384с.
2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.:Наука,1976.320с.
3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.:Наука,1972.496с.
4. Канторович Л. В., Акилов Г.П. Функциональный анализ. М.:Наука,1977. 742с.
5. Люстерник Л.А., Соболев В.И. Элементы функционального анализа. М.: Наука,1965. 520с.
6. Антоневич А.Б., Радыно Я.В. Функциональный анализ и интегральные уравнения. Мн.:Бгу,2003.430с.
7.Треногин В.А. Функциональный анализ. М.:Наука,1980.496с.
8. Морен К. Методы гильбертова пространства. М.:Мир,1965.572с.
9. Треногин В.А., Писаревский Б.М., Соболева Т.С. Задачи и упражнения по функциональному анализу. М.:ФИЗМАТЛИТ,2002.240с.
10. Городецкий В.В., Нагнибеда Н.И., Настиев П.П. Методы решения задач по функциональному анализу. Киев:Вища шк.1990.479с.
11. Петров В.А., Виленкин Н.Я., Граев М.И. Элементы функционального анализа в задачах. М.ПРОСВЕЩЕНИЕ,1978.128с.
12. Эминов С.И.Функциональный анализ. Часть 1. Метрические пространства. В. Новгород 2008.

 , то
, то  , т.е.
, т.е. 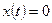 на отрезке
на отрезке  . Но, вообще говоря,
. Но, вообще говоря,  на всем отрезке
на всем отрезке  .
.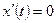 на отрезке
на отрезке 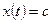 , которая может не обращаться в нуль.
, которая может не обращаться в нуль. и
и  должно выполняться соотношение
должно выполняться соотношение .
. ,
, 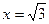 , получаем
, получаем  , что неверно.
, что неверно.
 . Так как это неравенство справедливо при всех
. Так как это неравенство справедливо при всех 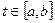 , то получим
, то получим
 .
. пробегает от 0 до
пробегает от 0 до  , получим неравенство треугольника.
, получим неравенство треугольника. . Пусть
. Пусть  - произвольное неотрицательное число. Положим
- произвольное неотрицательное число. Положим  , тогда
, тогда  . Утверждение доказано.
. Утверждение доказано.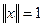 . Тогда элемент
. Тогда элемент  лежит на сфере.
лежит на сфере. имеем
имеем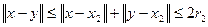 .
.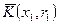 есть такая точка
есть такая точка 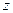 , что
, что  . Точка
. Точка 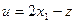 также лежит в указанном шаре, причем
также лежит в указанном шаре, причем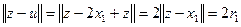 .
. и
и  , то с одной стороны
, то с одной стороны  , а с другой стороны
, а с другой стороны  , так как
, так как  . Полученное противоречие и доказывает утверждение задачи.
. Полученное противоречие и доказывает утверждение задачи. , т.е.
, т.е. 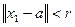 ,
,  . Возьмем произвольный элемент вида
. Возьмем произвольный элемент вида  ,
,  . Имеем
. Имеем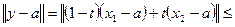
 .
. , и, следовательно,
, и, следовательно, 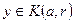 .
. и
и  . Рассмотрим произвольный шар
. Рассмотрим произвольный шар  . Точки вид
. Точки вид  попадают в шар
попадают в шар 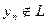 , в противном случае и точка
, в противном случае и точка  принадлежала бы линейному многообразию
принадлежала бы линейному многообразию  . Следовательно, никакой шар не может принадлежать данному многообразию
. Следовательно, никакой шар не может принадлежать данному многообразию  существует счетный алгебраический базис
существует счетный алгебраический базис  . Это означает, что каждый элемент представляется в виде конечной суммы
. Это означает, что каждый элемент представляется в виде конечной суммы ,
, .
. замкнуто и по определению алгебраического базиса
замкнуто и по определению алгебраического базиса .
.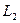 имеет размерность один, далее утверждение доказывается методом математической индукции
имеет размерность один, далее утверждение доказывается методом математической индукции и вектором
и вектором  . Требуется доказать замкнутость
. Требуется доказать замкнутость  , то
, то  и поэтому замкнуто. Пусть теперь
и поэтому замкнуто. Пусть теперь  . Согласно предложения 19 из второй главы,
. Согласно предложения 19 из второй главы,  . Линейное многообразие
. Линейное многообразие  , где
, где  . Докажем, что
. Докажем, что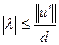 . (5.1)
. (5.1) , если
, если  , если же
, если же 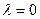 , то неравенство (5.1) очевидно.
, то неравенство (5.1) очевидно.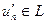 и
и 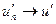 , когда
, когда 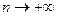 ; требуется доказать, что
; требуется доказать, что  . Пусть
. Пусть  ,
,  . Применяя неравенство (6.1) к вектору
. Применяя неравенство (6.1) к вектору  , получим
, получим ,
, 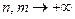 .
. стремится к некоторому пределу
стремится к некоторому пределу  .
. . Итак,
. Итак,  , что и требовалось доказать.
, что и требовалось доказать. . И поскольку в этом пространстве имеются другие функции, помимо многочленов, то линейное многообразие многочленов не является замкнутым;
. И поскольку в этом пространстве имеются другие функции, помимо многочленов, то линейное многообразие многочленов не является замкнутым; сходится к
сходится к  и каждый элемент последовательности удовлетворяет условию
и каждый элемент последовательности удовлетворяет условию 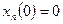 , то и предельная функция удовлетворяет этому же условию, те.
, то и предельная функция удовлетворяет этому же условию, те. 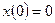 .
. для каждого элемента последовательности, то и для предельного элемента справедливо равенство:
для каждого элемента последовательности, то и для предельного элемента справедливо равенство:  .
.
 при
при 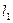 . Это означает, что для любого
. Это означает, что для любого  существует
существует  такое, что для всех
такое, что для всех  справедливо неравенство
справедливо неравенство .
. .
. . И поскольку
. И поскольку 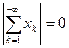 , т.е.
, т.е. 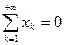 . Следовательно,
. Следовательно,  .
. , начиная со второго, равны числу
, начиная со второго, равны числу 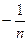 .
. . В самом деле
. В самом деле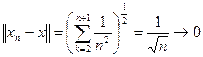 при
при  . Следовательно, линейное многообразие
. Следовательно, линейное многообразие  . Утверждение доказано.
. Утверждение доказано.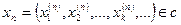
 . Для любого
. Для любого 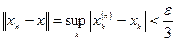
 ,
,  .
. , то последовательность
, то последовательность  сходится. Поэтому существует
сходится. Поэтому существует  такое, что для всех
такое, что для всех  будет
будет .
. .
. является сходящейся. Утверждение доказано.
является сходящейся. Утверждение доказано. одномерное подпространство, порожденное постоянной функцией
одномерное подпространство, порожденное постоянной функцией  . Легко увидеть, что
. Легко увидеть, что  . Произвольную
. Произвольную  представим в виде
представим в виде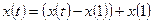 .
. функций. Очевидно,
функций. Очевидно,  . Докажем замкнутость. Возьмем последовательность четных функций
. Докажем замкнутость. Возьмем последовательность четных функций  ,
,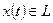 . Аналогично доказывается, что множество
. Аналогично доказывается, что множество  , элементами которого являются последовательности вида
, элементами которого являются последовательности вида .
. , если
, если  дл. Следовательно, каждая точка множества
дл. Следовательно, каждая точка множества  . Тогда
. Тогда  , но ни при каком
, но ни при каком  , очевидно,
, очевидно, 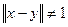
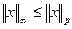 . Далее из определения нормы следует, что
. Далее из определения нормы следует, что  ,
,  . Отсюда
. Отсюда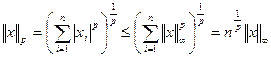 .
.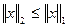 . Представим произвольную функцию
. Представим произвольную функцию  в виде
в виде .
. ,
,  .
.
 . Тогда из неравенств
. Тогда из неравенств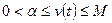
 ,
, ,
,  . Тогда
. Тогда , при
, при 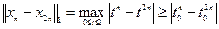 .
.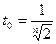 , получим отсюда, что
, получим отсюда, что .
. подчинена норме
подчинена норме 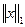 , проверяется непосредственно:
, проверяется непосредственно: .
. имеем
имеем . (5.2)
. (5.2) в пределах от
в пределах от  до 1 и изменяя порядок интегрирования в двойном интеграле, получим
до 1 и изменяя порядок интегрирования в двойном интеграле, получим . (5.3)
. (5.3) , (5.4)
, (5.4) ограничена в квадрате
ограничена в квадрате  .
.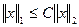
 . Покажем, что это свойство в нашем случае не выполняется. Взяв
. Покажем, что это свойство в нашем случае не выполняется. Взяв  , найдем
, найдем  ,
,  . Следовательно,
. Следовательно, .
. , где
, где  ,
,  ,…,
,…,  ,…. Поскольку элементы ненулевые, то
,…. Поскольку элементы ненулевые, то  . Положим
. Положим 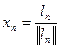 . Согласно второй аксиомы для нормы
. Согласно второй аксиомы для нормы  .
. ,когда
,когда  стремится к нулю. Но норма
стремится к нулю. Но норма  , эта же последовательность не стремится к нулю по норме. Утверждение доказано.
, эта же последовательность не стремится к нулю по норме. Утверждение доказано. многочленов, где
многочленов, где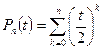 .
. - фундаментальная последовательность в пространстве
- фундаментальная последовательность в пространстве 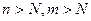
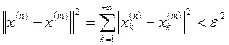 . (5.5)
. (5.5)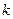
 ,
, - фундаментальна и, следовательно, сходится к некоторому пределу
- фундаментальна и, следовательно, сходится к некоторому пределу  :
: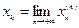 .
. . Далее из (5.5) для любого натурального
. Далее из (5.5) для любого натурального 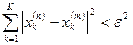 .
. . (5.6)
. (5.6)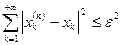 . (5.7)
. (5.7) и
и  вытекает сходимость ряда
вытекает сходимость ряда  .
. .
. . (5.8)
. (5.8) (5.9)
(5.9) . (5.10)
. (5.10) .
. следует ограниченность последовательности
следует ограниченность последовательности  сходится к элементу
сходится к элементу  при
при  при
при  . Выберем подпоследовательность
. Выберем подпоследовательность  так, чтобы
так, чтобы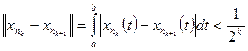
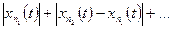 (5.11)
(5.11) . По теореме Леви из теории интеграла Лебега [2,3] ряд (5.11) сходится почти всюду на отрезке
. По теореме Леви из теории интеграла Лебега [2,3] ряд (5.11) сходится почти всюду на отрезке 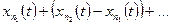
 .
.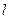 имеем
имеем .
. . В результате получаем
. В результате получаем ,
, и
и  по норме. А из того, что фундаментальная последовательность содержит подпоследовательность, сходящуюся к некоторому пределу, следует, что и сама последовательность сходится к тому же пределу.
по норме. А из того, что фундаментальная последовательность содержит подпоследовательность, сходящуюся к некоторому пределу, следует, что и сама последовательность сходится к тому же пределу. так, чтобы
так, чтобы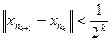
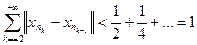 .
. и поэтому образуют расходящуюся последовательность. Утверждение доказано.
и поэтому образуют расходящуюся последовательность. Утверждение доказано. , к некоторому элементу
, к некоторому элементу  . И поскольку
. И поскольку  .
. , сходящаяся к
, сходящаяся к  из множества
из множества  и, следовательно,
и, следовательно,  при
при  стабилизируются и тогда соответственно шары совпадают ил же, наконец,
стабилизируются и тогда соответственно шары совпадают ил же, наконец, 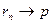 ,
,  . В последнем случае последовательность шаров с теми же центрами, радиусы которых равны
. В последнем случае последовательность шаров с теми же центрами, радиусы которых равны 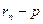 , является вложенной и по доказанному имеет непустое пересечение. Утверждение доказано.
, является вложенной и по доказанному имеет непустое пересечение. Утверждение доказано. ,
, .
. принадлежат одному классу смежности
принадлежат одному классу смежности  . Тогда
. Тогда 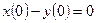 или
или  . Взяв в каждом классе смежности по представителю
. Взяв в каждом классе смежности по представителю 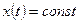 , получим взаимно однозначное соответствие между множеством действительных чисел
, получим взаимно однозначное соответствие между множеством действительных чисел  и фактор-пространством
и фактор-пространством  . Указанное соответствие является изоморфизмом.
. Указанное соответствие является изоморфизмом.


