Банахово пространство с базисом
Определение 8. Пусть
Однозначность этого представления равносильна условию, что
тогда и только тогда, когда Рассмотрим примеры банаховых пространств с базисомШаудера. Пример 1. Рассмотрим пространство
В самом деле,
и потому
как остаток сходящегося ряда. Отсюда
И если
то
Отсюда следует, что Пример 2. Рассмотрим пространство непрерывных функций
где
Разложение непрерывной функции в ряд по введенному базису имеет вид
где
График частичной суммы
есть ломаная линия с
ЗАДАЧИ В рассматриваемых ниже задачах предполагается, что нормированное пространстве 1. Можно ли на линейном многообразии непрерывных функций
2. Можно ли на линейном многообразии непрерывно дифференцируемых на
3. Можно ли на линейном многообразии непрерывно дифференцируемых на
4. Задает ли функция 5. В линейном многообразии
где 6. Согласно определения, норма задает отображение нормированного пространства во множество неотрицательных чисел. Доказать, что это отображение сюръективно. 7. Доказать, что никакая сфера 8. Пусть
9. Доказать, что шар (замкнутый шар) в произвольном линейном нормированном пространстве является выпуклым множеством. 10. Пусть 11. Доказать, что в бесконечномерном банаховом пространстве не может существовать счетного алгебраического базиса. 12. Пусть 13. Образуют ли в пространстве a) многочлены; б) многочлены степени меньше или равно фиксированного в) функции г) функции 14. Доказать, что линейное многообразие
Является подпространством в нормированном пространстве 15. Доказать, что линейное многообразие
не является подпространством в нормированном пространстве 16. В пространстве 17. В пространстве a) b) существует такое одномерное подпространство 18. Представить пространстве 19. Пусть
20. Доказать непосредственно, не привлекая теорему 2 из второй главы, эквивалентность следующих двух норм в в пространстве
21. Эквивалентны ли в пространстве
и
22. Доказать, что в линейном многообразии непрерывных на функций норма где 23. Доказать, что в линейном многообразии непрерывных на функций нормы
и
не эквивалентны. 24. Эквивалентны ли в пространстве
и
25. Рассмотрим метрическое пространство
Доказать, в пространстве
26. Доказать, что в пространстве 27. В линейном пространстве многочленов, рассматриваемом на
Доказать неполноту получаемых нормированных пространств. 28. Доказать полноту пространств последовательностей 29. Доказать полноту пространства 30. Доказать полноту пространства 31. Доказать, что в неполном нормированном пространстве 32. Доказать, что подмножество 33. Доказать, что в банаховом пространстве любая последовательность непустых вложенных замкнутых шаров имеет непустое пересечение. 34. Доказать, что в банаховом пространстве последовательность непустых ограниченных вложенных множеств может иметь пустое пересечение. 35. В пространстве
|

 - бесконечномерное банахово пространство. Последовательность элементов
- бесконечномерное банахово пространство. Последовательность элементов  из
из 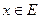 можно представить однозначно в виде
можно представить однозначно в виде .
.
 для всех
для всех  .
. и элементы
и элементы  ,
,  ,…. Покажем, что для любого
,…. Покажем, что для любого  изпространства
изпространства 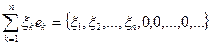
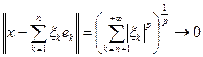 ,
,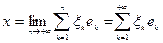 .
. ,
, .
.
 и взаимная однозначность доказана.
и взаимная однозначность доказана.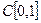 . Базис Шаудера состоит из системы функций
. Базис Шаудера состоит из системы функций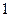 ,
,  ,
,  ,
, 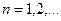 и
и  , (3.9)
, (3.9)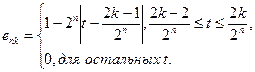 (3.10)
(3.10) , (3.11)
, (3.11)
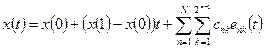
 вершинами, лежащими на кривой
вершинами, лежащими на кривой  в точках с равностоящим абсциссами. Можно показать, что функции (3.8) образуют базис Шаудера в пространстве
в точках с равностоящим абсциссами. Можно показать, что функции (3.8) образуют базис Шаудера в пространстве 
 за норму элемента
за норму элемента  .
. функций за норму элемента
функций за норму элемента  .
. .
. норму на числовой прямой?
норму на числовой прямой? функций, которые непрерывны на отрезке
функций, которые непрерывны на отрезке  -го порядка включительно введем норму
-го порядка включительно введем норму ,
, - производная функции
- производная функции  не может быть пустым множеством.
не может быть пустым множеством.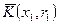 и
и  - два замкнутых шара. Доказать, что если
- два замкнутых шара. Доказать, что если , то
, то  .
.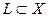 - линейное многообразие,
- линейное многообразие,  . Доказать, что
. Доказать, что  не содержит никакого шара.
не содержит никакого шара. - подпространства. Доказать, что если хотя бы одно их них конечномерно, то
- подпространства. Доказать, что если хотя бы одно их них конечномерно, то  - подпространство.
- подпространство. подпространство следующие линейные многообразия функций:
подпространство следующие линейные многообразия функций: ;
; .
.
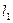 .
. .
. всех ограниченных числовых последовательностей
всех ограниченных числовых последовательностей  с нормой
с нормой  рассмотрим линейное многообразие
рассмотрим линейное многообразие 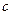 сходящихся последовательностей. Доказать, что
сходящихся последовательностей. Доказать, что  . Доказать, что:
. Доказать, что: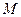 , что
, что  .
. в виде прямой суммы двух бесконечномерных пространств.
в виде прямой суммы двух бесконечномерных пространств. является замкнутым множеством в нормированном пространстве
является замкнутым множеством в нормированном пространстве  и
и 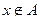 . Всегда ли найдется такой элемент
. Всегда ли найдется такой элемент  , что
, что .
. :
: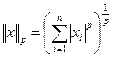 ,
,  ,
,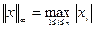 .
. нормы
нормы
 ?
?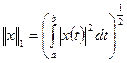 эквивалентна норме
эквивалентна норме  ,
, непрерывна на
непрерывна на 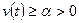 на
на 


 нормы
нормы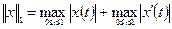
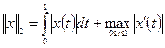 ?
?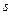 всех последовательностей, в котором расстояние между элементами
всех последовательностей, в котором расстояние между элементами  определяется по формуле
определяется по формуле .
.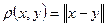 .
. .
. .
. рассмотрим подпространство
рассмотрим подпространство  . Доказать, что фактор-пространство
. Доказать, что фактор-пространство  изоморфно
изоморфно  .
.


