Множества первой и второй категорииВ банаховых пространствах справедлив аналог известного принципа вложенных отрезков. Теорема 3. Для того чтобы нормированное пространство Доказательство этой теоремы имеется в [4], поэтому здесь не приводится. Далее приведем важные определения и теорему Бэра. Определение 5. Множество Можно показать, что определение 5 эквивалентно следующему определению. Определение 5 (эквивалентное определение). Множество Определение 6. Множество Определение 7. Множество, на являющееся множеством первой категории, называется множеством второй категории. Теорема 4 (Бэр). Всякое банахово пространство является множеством второй категории. Доказательство этой теоремы также имеется в [12].
|
было полным, необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стремятся к нулю, имела непустое пересечение.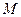
называется нигде не плотным в нормированном пространстве 
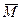не содержит ни одного открытого шара. 
