Лемма Рисса. Пусть  - подпространство нормированного пространства
- подпространство нормированного пространства  , причем
, причем  . Для любого числа
. Для любого числа  существует элемент
существует элемент  такой, что
такой, что
 ,
, 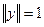 . (2.14)
. (2.14)
Доказательство. Поскольку  , то существует элемент
, то существует элемент  . Положим
. Положим
 .
.
Из предложения 19 следует, что  . По определению
. По определению  , для любого числа
, для любого числа  найдется элемент
найдется элемент 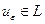 такой, что
такой, что
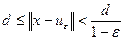 .
.
Введем в рассмотрение элемент
 ,
, 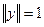 ,
,
и докажем, что  - искомый элемент. Вначале заметим, что
- искомый элемент. Вначале заметим, что  , ибо в противном случае
, ибо в противном случае  , откуда
, откуда  , а это противоречит выбору элемента
, а это противоречит выбору элемента  . Далее оценим расстояние от
. Далее оценим расстояние от  до
до  :
:
 .
.
При выводе этого неравенства учли, что  , а также неравенство
, а также неравенство  для
для  . Лемма доказана.
. Лемма доказана.
Рассмотрим одно из применений леммы Рисса. Известно из курса математического анализа, что всякая ограниченная последовательность точек из  содержит сходящуюся подпоследовательность. В бесконечномерном пространстве не из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность. С помощью леммы Рисса построим такой пример.
содержит сходящуюся подпоследовательность. В бесконечномерном пространстве не из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность. С помощью леммы Рисса построим такой пример.
Пример 1. Рассмотрим бесконечномерное нормированное пространство  и возьмем произвольный элемент
и возьмем произвольный элемент  . Обозначим через
. Обозначим через  линейную оболочку
линейную оболочку  , т.е. совокупность элементов вида
, т.е. совокупность элементов вида  . Пространство
. Пространство  является бесконечномерным, поэтому
является бесконечномерным, поэтому  . По лемме Рисса найдется элемент
. По лемме Рисса найдется элемент  такой, что
такой, что
 ,
,  .
.
Образуем линейную оболочку элементов  и
и  , которую обозначим через
, которую обозначим через  . Заметим, что эта линейная оболочка является замкнутым подпространством, как следует из предложения 18. Продолжая процесс, получим последовательность элементов
. Заметим, что эта линейная оболочка является замкнутым подпространством, как следует из предложения 18. Продолжая процесс, получим последовательность элементов 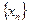 и подпространств
и подпространств  , таких что
, таких что
 ,
,  ,
,  .
.
Построенная последовательность 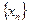 ограничена, но как следует из неравенства
ограничена, но как следует из неравенства
 ,
,  ,
,  ,
,
ни сама последовательность, ни какая-либо ее подпоследовательность не могут сходиться.

 - подпространство нормированного пространства
- подпространство нормированного пространства  , причем
, причем  . Для любого числа
. Для любого числа  существует элемент
существует элемент  такой, что
такой, что ,
, 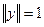 . (2.14)
. (2.14) . Положим
. Положим .
. . По определению
. По определению  , для любого числа
, для любого числа 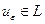 такой, что
такой, что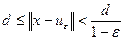 .
. ,
,  - искомый элемент. Вначале заметим, что
- искомый элемент. Вначале заметим, что  , откуда
, откуда  , а это противоречит выбору элемента
, а это противоречит выбору элемента  . Далее оценим расстояние от
. Далее оценим расстояние от  .
. , а также неравенство
, а также неравенство  для
для  . Лемма доказана.
. Лемма доказана. содержит сходящуюся подпоследовательность. В бесконечномерном пространстве не из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность. С помощью леммы Рисса построим такой пример.
содержит сходящуюся подпоследовательность. В бесконечномерном пространстве не из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность. С помощью леммы Рисса построим такой пример. . Обозначим через
. Обозначим через  линейную оболочку
линейную оболочку  , т.е. совокупность элементов вида
, т.е. совокупность элементов вида  . Пространство
. Пространство  . По лемме Рисса найдется элемент
. По лемме Рисса найдется элемент  такой, что
такой, что ,
,  .
.  . Заметим, что эта линейная оболочка является замкнутым подпространством, как следует из предложения 18. Продолжая процесс, получим последовательность элементов
. Заметим, что эта линейная оболочка является замкнутым подпространством, как следует из предложения 18. Продолжая процесс, получим последовательность элементов 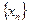 и подпространств
и подпространств  , таких что
, таких что ,
,  ,
,  .
. ,
,  ,
, 


