Ряды в нормированных и банаховых пространствах
Из элементов нормированного пространства
и назовем частичной суммой ряда (3.3) сумму первых
Определение 3. Ряд (3.3) называется сходящимся, если последовательность
называется суммой ряда и обозначается
Определение 4. Если сходится числовой ряд, составленный из норм
то ряд (3.3) называется абсолютно сходящимся. В курсе математического анализа для числовых рядов доказывается, что всякий абсолютно сходящийся числовой ряд сходится. Как следует из следующей теоремы, это свойство эквивалентно полноте. Теорема 2. Нормированное пространство является банаховым тогда и только тогда, когда в нем каждый абсолютно сходящийся ряд сходится. Доказательство необходимости. Пусть
Таким образом, последовательность частичных сумм фундаментальна и поэтому сходится в силу полноты пространства
к пределу, получим
которое является обобщением неравенства треугольника для норм. Доказательство достаточности. Пусть в нормированном пространстве любой абсолютно сходящийся ряд сходится. Возьмем фундаментальную последовательность
После того, как выбраны
Продолжая этот процесс, построим подпоследовательность
А теперь составим ряд
Этот ряд сходится абсолютно, согласно оценке (3.6), тогда он сходится по условию теоремы. С другой стороны, частичная сумма последнего ряда
равна элементу
|

 составим формальный ряд
составим формальный ряд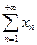 (3.3)
(3.3) элементов, т.е. выражение
элементов, т.е. выражение .
. частичных сумм. При этом элемент
частичных сумм. При этом элемент
 .
. 
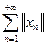 , (3.4)
, (3.4) имеем
имеем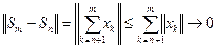 , когда
, когда  .
.
 , (3.5)
, (3.5)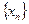 . В силу фундаментальности, найдется такой номер
. В силу фундаментальности, найдется такой номер  , что
, что ,
,  .
. , найдем
, найдем  так, чтобы
так, чтобы ,
,  .
. такую, что
такую, что ,
,  . (3.6)
. (3.6) .
.
 . Таким образом, сходится подпоследовательность
. Таким образом, сходится подпоследовательность 


