Определение 18. Пусть  - подпространство нормированного пространства
- подпространство нормированного пространства  . Определим расстояние от точки
. Определим расстояние от точки  до подпространства
до подпространства  по формуле
по формуле
 . (2.13) Имеет место предложение.
. (2.13) Имеет место предложение.
Предложение 19. Если  , то
, то  , если же
, если же  , то
, то  .
.
Доказательство. Если  , то, приняв
, то, приняв  , получим, что
, получим, что  ,т.е.
,т.е.
Пусть теперь  . Допустим противное, что
. Допустим противное, что  . Тогда по определению
. Тогда по определению  для любого натурального числа
для любого натурального числа  найдется такой элемент
найдется такой элемент  , что
, что  . Отсюда
. Отсюда  , когда
, когда  . Вследствие замкнутости
. Вследствие замкнутости  также
также  , но по условию
, но по условию  . Полученное противоречие и доказывает предложение.
. Полученное противоречие и доказывает предложение.
Число  характеризует наилучшую аппроксимацию элемента
характеризует наилучшую аппроксимацию элемента  с помощью элементов подпространства
с помощью элементов подпространства  . Имеет место теорема.
. Имеет место теорема.
Теорема 3. Пусть  - конечномерное подпространство нормированного пространства
- конечномерное подпространство нормированного пространства  . Для любого
. Для любого  существует (возможно, не единственный) такой элемент
существует (возможно, не единственный) такой элемент  , что
, что
 .
.
Доказательство. Предполагаем, что  , тогда
, тогда  . Пусть
. Пусть  - базис на
- базис на  и
и  - разложение
- разложение  по базису. Введем на
по базису. Введем на  вторую норму:
вторую норму:
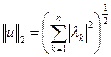 .
.
С этой нормой пространство  будем отождествлять с пространством
будем отождествлять с пространством  , как и при доказательстве теоремы 2. Вследствие конечномерности
, как и при доказательстве теоремы 2. Вследствие конечномерности  обе нормы эквивалентны: т.е. найдутся постоянные
обе нормы эквивалентны: т.е. найдутся постоянные  такие, что
такие, что
 .
.
Рассмотрим в  функцию
функцию 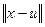 . Она непрерывна на
. Она непрерывна на  , поскольку для любых
, поскольку для любых 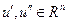
 .
.
Покажем, что  может достигаться только в шаре
может достигаться только в шаре
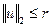 , где
, где  .
.
В самом деле, если  , то
, то
 .
.
Далее, шар 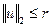 является в
является в  замкнутым и ограниченным множеством, а функция
замкнутым и ограниченным множеством, а функция 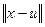 - непрерывна. Поэтому найдется
- непрерывна. Поэтому найдется  - наилучший элемент приближения
- наилучший элемент приближения 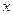 элементами из
элементами из  , на котором достигается наименьшее значение
, на котором достигается наименьшее значение 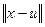 . Теорема доказана.
. Теорема доказана.
Определение 19. Нормированное пространство  называется строго нормированным, если в нем равенство
называется строго нормированным, если в нем равенство 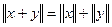 возможно только при
возможно только при  , где
, где  .
.
Теорема 4. В строго нормированном пространстве  для каждого элемента
для каждого элемента  и каждого подпространства
и каждого подпространства  может существовать не более одного наилучшего элемента приближения
может существовать не более одного наилучшего элемента приближения 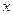 элементами из
элементами из  .
.
Доказательство. Допустим, что в строго нормированном пространстве  найдутся элемент
найдутся элемент 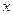 , подпространство
, подпространство  и элементы
и элементы  такие, что
такие, что
 .
.
Если  , то по первой аксиоме нормы
, то по первой аксиоме нормы  . Далее полагая
. Далее полагая  , имеем
, имеем
 .
.
Следовательно
 .
.
Но тогда
 .
.
В силу строгой нормированности  существует
существует  такое, что
такое, что  . Если
. Если  , то отсюда
, то отсюда
 ,
,
что невозможно, поскольку  . Следовательно,
. Следовательно,  , но тогда
, но тогда  . Теорема доказана.
. Теорема доказана.

 - подпространство нормированного пространства
- подпространство нормированного пространства  . Определим расстояние от точки
. Определим расстояние от точки  до подпространства
до подпространства  . (2.13) Имеет место предложение.
. (2.13) Имеет место предложение. , то
, то  , если же
, если же  , то
, то  .
. , получим, что
, получим, что  ,т.е.
,т.е.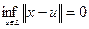
 для любого натурального числа
для любого натурального числа  найдется такой элемент
найдется такой элемент  , что
, что  . Отсюда
. Отсюда  , когда
, когда 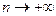 . Вследствие замкнутости
. Вследствие замкнутости  характеризует наилучшую аппроксимацию элемента
характеризует наилучшую аппроксимацию элемента 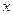 с помощью элементов подпространства
с помощью элементов подпространства  , что
, что .
. . Пусть
. Пусть  - базис на
- базис на  - разложение
- разложение  по базису. Введем на
по базису. Введем на 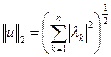 .
. , как и при доказательстве теоремы 2. Вследствие конечномерности
, как и при доказательстве теоремы 2. Вследствие конечномерности  такие, что
такие, что .
.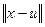 . Она непрерывна на
. Она непрерывна на 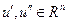
 .
. может достигаться только в шаре
может достигаться только в шаре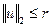 , где
, где  .
. , то
, то .
.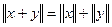 возможно только при
возможно только при  , где
, где  .
. такие, что
такие, что .
. , то по первой аксиоме нормы
, то по первой аксиоме нормы  . Далее полагая
. Далее полагая  , имеем
, имеем .
. .
. .
. . Если
. Если  , то отсюда
, то отсюда ,
, , но тогда
, но тогда