Поскольку нормированные пространства в то же время являются метрическими, то все понятия метрических пространств переносятся на нормированные пространства. Здесь приведем определения открытых и замкнутых множеств и их свойства. Все предложения этого пункта, как правило, приводятся без доказательств, их можно найти в пособии [12].
Определение 4. Открытым шаром 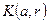 в нормированном пространстве
в нормированном пространстве  с центром в точке
с центром в точке  и радиуса
и радиуса  называется множество всех таких точек
называется множество всех таких точек  , что
, что 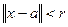 .
.
Замкнутым шаром  называется множество всех таких точек
называется множество всех таких точек  , что
, что  .
.
Определение 5. Множество  называется открытым в нормированном пространстве
называется открытым в нормированном пространстве  , если для любого
, если для любого 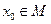 найдется такое число
найдется такое число  , что верно включение
, что верно включение  .
.
Определение 6. Окрестностью точки  называется любое открытое множество, содержащее
называется любое открытое множество, содержащее  .
.
Предложение 7. Открытый шар является открытым множеством.
Открытый шар является окрестностью каждой своей точки.
Предложение 8. Объединение любого числа открытых множеств открыто. Пересечение любого конечного числа открытых множеств есть открытое множество.
Определение 7. Множество  в метрическом пространстве
в метрическом пространстве  называется замкнутым, если его дополнение
называется замкнутым, если его дополнение  открыто.
открыто.
Предложение 9. Пересечение любого числа замкнутых множеств замкнуто. Объединение конечного числа замкнутых множеств замкнуто.
Определение 8. Точка  называется точкой прикосновения множества
называется точкой прикосновения множества  , если каждая окрестность точки
, если каждая окрестность точки  содержит хотя бы одну точку множества
содержит хотя бы одну точку множества  .
.
Определение 9. Точка  называется предельной точкой множества
называется предельной точкой множества  , если каждая окрестность точки
, если каждая окрестность точки  содержит хотя бы одну точку множества
содержит хотя бы одну точку множества  , отличную от точки
, отличную от точки  .
.
Предложение 10. Множество  является замкнутым тогда и только тогда, когда оно содержит все свои точки прикосновения.
является замкнутым тогда и только тогда, когда оно содержит все свои точки прикосновения.
Предложение11. Множество  является замкнутым тогда и только тогда, когда оно содержит все свои предельные точки.
является замкнутым тогда и только тогда, когда оно содержит все свои предельные точки.
Определение 10. Множество всех точек прикосновения множества  называется замыканием множества
называется замыканием множества  и обозначается символом
и обозначается символом 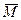 .
.
Предложение 12. Имеет место соотношение  .
.
Из этого предложения следует, что множество 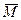 замкнуто.
замкнуто.
Дадим еще одно важное определение.
Определение 11. Точка  , принадлежащая
, принадлежащая  ,называется изолированной точкой этого множества, если в некоторой ее окрестности нет точек из
,называется изолированной точкой этого множества, если в некоторой ее окрестности нет точек из  , отличных от
, отличных от  .
.
Всякая точка прикосновения множества  , как следует из определений, является либо предельной точкой для него, либо изолированной точкой этого множества. Отсюда следует, что замыкание
, как следует из определений, является либо предельной точкой для него, либо изолированной точкой этого множества. Отсюда следует, что замыкание 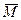 множества
множества  состоит из точек трех типов:
состоит из точек трех типов:
1) изолированные точки  ;
;
2) предельные точки множества  , принадлежащие
, принадлежащие  ;
;
3) предельные точки множества  , не принадлежащие
, не принадлежащие  .
.
Следовательно, замыкание 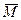 множества
множества  получается присоединением к
получается присоединением к  всех его предельных точек.
всех его предельных точек.
Предложение 13. Точка  нормированного пространства
нормированного пространства  принадлежит замыканию
принадлежит замыканию 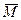 множества
множества  тогда и только тогда, когда существует последовательность точек
тогда и только тогда, когда существует последовательность точек  множества
множества  , сходящуюся к
, сходящуюся к  .
.
Доказательство. Пусть  . Если при этом
. Если при этом  , то в качестве последовательности можно взять
, то в качестве последовательности можно взять  . Далее полагаем, что
. Далее полагаем, что  . Тогда точка
. Тогда точка  является предельной точкой множества
является предельной точкой множества  , ему не принадлежащей. Поэтому в каждом шаре
, ему не принадлежащей. Поэтому в каждом шаре  , т.е. при любом
, т.е. при любом  , имеется хотя бы одна точка
, имеется хотя бы одна точка 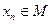 . В результате построили последовательность
. В результате построили последовательность 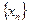 точек из множества
точек из множества  , сходящаяся к точке
, сходящаяся к точке  .
.
Верно и обратное: если  ,
, 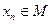 , то
, то  . Действительно, если
. Действительно, если  , то точка
, то точка  принадлежит открытому множеству
принадлежит открытому множеству  . Поэтому найдется открытый шар с центром в точке
. Поэтому найдется открытый шар с центром в точке  , целиком лежащий во множестве
, целиком лежащий во множестве  , т.е. не имеющий общих точек с множеством
, т.е. не имеющий общих точек с множеством  . А это противоречит тому, что последовательность точек
. А это противоречит тому, что последовательность точек  из множества
из множества  сходится к
сходится к  . Предложение доказано.
. Предложение доказано.
Далее нам потребуется еще одно понятие.
Определение 12. Точка 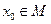 называется внутренней точкой множества
называется внутренней точкой множества  , если существует ее окрестность
, если существует ее окрестность  . Точка
. Точка  называется внешней точкой
называется внешней точкой  , если существует шар
, если существует шар  , не содержащий точек из
, не содержащий точек из  :
:  .
.
Точка  называется граничной точкой
называется граничной точкой  , если в любом шаре
, если в любом шаре  есть точки, принадлежащие
есть точки, принадлежащие  и точки, не принадлежащие
и точки, не принадлежащие  .
.

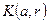 в нормированном пространстве
в нормированном пространстве  с центром в точке
с центром в точке  и радиуса
и радиуса  называется множество всех таких точек
называется множество всех таких точек  , что
, что 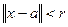 .
. называется множество всех таких точек
называется множество всех таких точек  .
. называется открытым в нормированном пространстве
называется открытым в нормированном пространстве 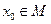 найдется такое число
найдется такое число  , что верно включение
, что верно включение  .
. .
. в метрическом пространстве
в метрическом пространстве  открыто.
открыто.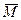 .
. .
. множества
множества  . Если при этом
. Если при этом  , то в качестве последовательности можно взять
, то в качестве последовательности можно взять  . Далее полагаем, что
. Далее полагаем, что  . Тогда точка
. Тогда точка  , т.е. при любом
, т.е. при любом  , имеется хотя бы одна точка
, имеется хотя бы одна точка 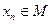 . В результате построили последовательность
. В результате построили последовательность 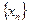 точек из множества
точек из множества  ,
,  , то точка
, то точка  . Поэтому найдется открытый шар с центром в точке
. Поэтому найдется открытый шар с центром в точке  называется внешней точкой
называется внешней точкой  , не содержащий точек из
, не содержащий точек из  .
. называется граничной точкой
называется граничной точкой 


