Определение 9. Линейные пространства  и
и  называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие, причем из того, что
называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие, причем из того, что  и
и  ,
,  следует, что
следует, что  и
и  .
.
Иначе говоря, это взаимно однозначное соответствие сохраняет алгебраические операции. Далее покажем, что всякое  - мерное линейное действительное пространство
- мерное линейное действительное пространство  изоморфно арифметическому пространству
изоморфно арифметическому пространству  . Для этого обозначим через
. Для этого обозначим через  базис пространства
базис пространства  , который существует в силу теоремы 1, и разложим произвольный элемент
, который существует в силу теоремы 1, и разложим произвольный элемент  по базису:
по базису:  .
.
Соотнося элементу  вектор
вектор  с компонентами
с компонентами  , получим взаимно однозначное соответствие между
, получим взаимно однозначное соответствие между  и
и  . Построенное соответствие является линейным изоморфизмом, поскольку, если
. Построенное соответствие является линейным изоморфизмом, поскольку, если  и
и  , то
, то 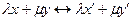 .
.
1.6. Фактор – пространства
Пусть  - линейное пространство и
- линейное пространство и  - некоторое линейное многообразие. Два элемента
- некоторое линейное многообразие. Два элемента  и
и  из
из  назовем эквивалентными, если их разность
назовем эквивалентными, если их разность  принадлежит
принадлежит  . Это отношение является рефлексивным, симметричным и транзитивным, т.е. определяет разбиение всех
. Это отношение является рефлексивным, симметричным и транзитивным, т.е. определяет разбиение всех  на классы. Совокупность всех таких классов называется фактор - пространством
на классы. Совокупность всех таких классов называется фактор - пространством  по
по  и обозначается
и обозначается  . Если
. Если  произвольный элемент из класса
произвольный элемент из класса  , то всякий другой элемент
, то всякий другой элемент  из
из  представим в виде
представим в виде  , где
, где  .
.
В множестве  всех классов можно ввести алгебраические операции. Пусть
всех классов можно ввести алгебраические операции. Пусть  и
и  два класса из
два класса из  . Выберем в каждом классе по представителю, например
. Выберем в каждом классе по представителю, например  и
и  соответственно, и назовем суммой классов
соответственно, и назовем суммой классов  и
и  тот класс
тот класс  , который содержит элемент
, который содержит элемент  , а произведением класса
, а произведением класса  на число
на число  тот класс, который содержит элемент
тот класс, который содержит элемент  .
.
Это определение, как легко проверить, не зависит от выбора элементов  и
и  - представителей классов
- представителей классов  и
и  . Введенные операции удовлетворяют аксиомам линейного пространства. Поэтому множество
. Введенные операции удовлетворяют аксиомам линейного пространства. Поэтому множество  становится линейным пространством, которое называется фактор – пространством, причем роль нулевого элемента играет линейное многообразие
становится линейным пространством, которое называется фактор – пространством, причем роль нулевого элемента играет линейное многообразие  .
.

 и
и  называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие, причем из того, что
называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие, причем из того, что  и
и  ,
,  следует, что
следует, что  и
и  .
. - мерное линейное действительное пространство
- мерное линейное действительное пространство  . Для этого обозначим через
. Для этого обозначим через  базис пространства
базис пространства  по базису:
по базису:  .
. с компонентами
с компонентами  , получим взаимно однозначное соответствие между
, получим взаимно однозначное соответствие между 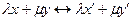 .
. - некоторое линейное многообразие. Два элемента
- некоторое линейное многообразие. Два элемента  и
и  из
из  принадлежит
принадлежит  . Это отношение является рефлексивным, симметричным и транзитивным, т.е. определяет разбиение всех
. Это отношение является рефлексивным, симметричным и транзитивным, т.е. определяет разбиение всех  . Если
. Если  , то всякий другой элемент
, то всякий другой элемент  , где
, где  .
. два класса из
два класса из  , который содержит элемент
, который содержит элемент  , а произведением класса
, а произведением класса  тот класс, который содержит элемент
тот класс, который содержит элемент  .
.


