И простейшие следствия
Определение 1. Непустое множество
1. 2. 3. Существует такой элемент 0, что 4. Для любого 5. 6. 7. 8. Если ограничиваться вещественными числами, то Приведем некоторые следствия из этих аксиом. Предложение 1. В любом линейном пространстве существует единственный нуль. Доказательство. Предположим, что в пространстве Полагая в аксиоме 3.
Затем, полагая в той же аксиоме
В силу коммутативности левые части (1.1) и (1.2) равны, а тогда и правые части равны, т.е. Предложение 2. В любом линейном пространстве для каждого элемента существует единственный противоположный элемент. Доказательство. Пусть для некоторого элемента
Поскольку равны левые части (1.3) и (1.4), то будут равны и правые части. Предложение доказано. Предложение 3. В любом линейном пространстве для каждого элемента имеет место равенство
Доказательство. Рассмотрим элемент
Сравнивая эти два соотношения, будем иметь
Прибавляя к обеим частям последнего равенства противоположный элемент, получим
т.е. Предложение 4. Для каждого элемента
Доказательство. Составим сумму
что и требовалось доказать.
|

 называется линейным пространством, если оно удовлетворяет условиям:
называется линейным пространством, если оно удовлетворяет условиям: Для любых двух элементов
Для любых двух элементов  однозначно определен третий элемент из
однозначно определен третий элемент из  .
. Для любого элемента
Для любого элемента  и любого числа
и любого числа  определено произведение
определено произведение 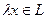 .
.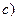 Для любых элементов
Для любых элементов  и любых чисел
и любых чисел  выполнены следующие восемь аксиом:
выполнены следующие восемь аксиом: (коммутативность).
(коммутативность). (ассоциативность).
(ассоциативность). для любого
для любого  , что
, что  (существование противоположного элемента).
(существование противоположного элемента).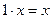 .
.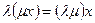 .
. .
. .
. ,
,  .
. и
и  , получим
, получим . (1.1)
. (1.1) и
и  , будем иметь
, будем иметь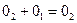 . (1.2)
. (1.2) . Предложение доказано.
. Предложение доказано. имеются два противоположных элемента
имеются два противоположных элемента  и
и  . Тогда с учетом аксиомы ассоциативности получим
. Тогда с учетом аксиомы ассоциативности получим  , (1.3)
, (1.3) . (1.4)
. (1.4) .
. и применим аксиомы 5. и 7. В результате получим
и применим аксиомы 5. и 7. В результате получим ,
, .
. .
. ,
, . Предложение доказано.
. Предложение доказано. .
. и используем предложение 3. В результате получим
и используем предложение 3. В результате получим ,
,


