Определение 9. Пусть  - линейное пространство,
- линейное пространство, 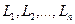 - принадлежащие ему линейные многообразия. Если каждый элемент
- принадлежащие ему линейные многообразия. Если каждый элемент  однозначно представим в виде
однозначно представим в виде
 ,
,  , (1.9)
, (1.9)
то говорят, что пространство  есть прямая сумма линейных многообразий
есть прямая сумма линейных многообразий 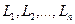 , а выражение (1.9) называется разложением элемента
, а выражение (1.9) называется разложением элемента  по элементам из
по элементам из 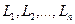 . При этом пишут
. При этом пишут
 . (1.10)
. (1.10)
Предложение 6. Если  , то
, то  .
.
Доказательство. В самом деле, если бы 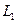 и
и  содержали другой общий элемент
содержали другой общий элемент  , то для элемента
, то для элемента  , имеющего представление
, имеющего представление
 ,
,  ,
,  ,
,
было бы также справедливо представление
 ,
,  ,
,  ,
,
отличное от первого. А это противоречит условию. Предложение доказано.
Справедливо обратное утверждение.
Предложение 7. Если любой элемент  может быть представлен в виде
может быть представлен в виде
 ,
,  ,
,  , (1.11)
, (1.11)
и  , то
, то  .
.
Доказательство. Необходимо доказать однозначность представления (1.11).
Но если
 ,
,  ,
,  ,
,
то
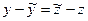 ,
,  ,
,  .
.
В силу условия предложения отсюда следует, что  , т.е.
, т.е.  ,
,  . Предложение доказано.
. Предложение доказано.
Приведем еще несколько определений, которые потребуются в дальнейшем.
Определение 10. Пусть  и
и  - множества пространства
- множества пространства  . Через
. Через  обозначается множество всех элементов вида
обозначается множество всех элементов вида  , где
, где  и
и  . Точно также, если
. Точно также, если  множество чисел, то через
множество чисел, то через  обозначается множество всех элементов вида
обозначается множество всех элементов вида  , где
, где  и
и  .
.
Заметим, что, вообще говоря,  , а только
, а только  .
.
Определение 11. Множество  называется выпуклым, если вместе с точками
называется выпуклым, если вместе с точками  и
и  оно содержит весь отрезок
оно содержит весь отрезок  , соединяющий эти точки, т.е. множество точек
, соединяющий эти точки, т.е. множество точек  при
при  .
.
1.8.  Лемма Цорна. Существование
Лемма Цорна. Существование

 - линейное пространство,
- линейное пространство, 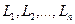 - принадлежащие ему линейные многообразия. Если каждый элемент
- принадлежащие ему линейные многообразия. Если каждый элемент  однозначно представим в виде
однозначно представим в виде ,
,  , (1.9)
, (1.9) по элементам из
по элементам из  . (1.10)
. (1.10) , то
, то  .
.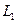 и
и  содержали другой общий элемент
содержали другой общий элемент  , то для элемента
, то для элемента  ,
,  ,
,  ,
, ,
,  ,
,  ,
, ,
,  ,
,  ,
,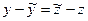 ,
,  ,
,  .
. , т.е.
, т.е.  ,
,  . Предложение доказано.
. Предложение доказано. и
и  - множества пространства
- множества пространства  обозначается множество всех элементов вида
обозначается множество всех элементов вида  , где
, где  и
и  . Точно также, если
. Точно также, если  множество чисел, то через
множество чисел, то через  обозначается множество всех элементов вида
обозначается множество всех элементов вида  , где
, где  и
и  , а только
, а только  .
. называется выпуклым, если вместе с точками
называется выпуклым, если вместе с точками  оно содержит весь отрезок
оно содержит весь отрезок  , соединяющий эти точки, т.е. множество точек
, соединяющий эти точки, т.е. множество точек  при
при  .
. Лемма Цорна. Существование
Лемма Цорна. Существование


