Определение 7. Непустое подмножество  линейного пространства
линейного пространства  называется линейным многообразием, если из
называется линейным многообразием, если из  ,
,  следует, что
следует, что  .
.
Покажем, что линейное многообразие само является линейным пространством. Аксиомы 1,2, а также 5-8 выполняются, поскольку они выполняются для всех элементов пространства  . Остается проверить аксиомы 3,4.
. Остается проверить аксиомы 3,4.
Возьмем  ; поскольку
; поскольку  , то нулевой элемент принадлежит
, то нулевой элемент принадлежит  .
.
Теперь возьмем  ; поскольку
; поскольку  есть элемент, противоположный элементу
есть элемент, противоположный элементу  , то подмножество
, то подмножество  вместе с каждым элементом
вместе с каждым элементом  содержит и противоположный элемент. Следовательно, выполнены все аксиомы линейного пространства. Приведем примеры линейных многообразий.
содержит и противоположный элемент. Следовательно, выполнены все аксиомы линейного пространства. Приведем примеры линейных многообразий.
Пример 1. Нулевой элемент пространства  образует наименьшее, возможное линейное многообразие пространства
образует наименьшее, возможное линейное многообразие пространства  .
.
Пример 2. Все пространство  - наибольшее, возможное линейное многообразие пространства
- наибольшее, возможное линейное многообразие пространства  .
.
Пример 3. Пусть  - линейное пространство и
- линейное пространство и  - его ненулевой элемент. Элементы вида
- его ненулевой элемент. Элементы вида  , где
, где  пробегает все числа, образует линейное многообразие.
пробегает все числа, образует линейное многообразие.
Пример 4. Множество всех многочленов 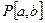 образует линейное многообразие в линейном пространстве непрерывных функций.
образует линейное многообразие в линейном пространстве непрерывных функций.
Пример 5. Пространство  является линейным многообразием в линейном пространстве ограниченных последовательностей.
является линейным многообразием в линейном пространстве ограниченных последовательностей.
Определение 8. Пусть дано некоторое подмножество  линейного пространства
линейного пространства  . Линейной оболочкой
. Линейной оболочкой  называется совокупность всевозможных линейных комбинаций, каждая из которых составлена из конечного числа элементов, принадлежащих
называется совокупность всевозможных линейных комбинаций, каждая из которых составлена из конечного числа элементов, принадлежащих  . Линейную оболочку множества
. Линейную оболочку множества  будем обозначать через
будем обозначать через  .
.
Покажем, что линейная оболочка является линейным многообразием. В самом деле, если  и
и  принадлежат
принадлежат  , то
, то
 ,
,  ,
,  .
.
Тогда
 ,
, 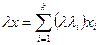 ,
,
т.е. сумма двух элементов и произведение элемента на число являются линейными комбинациями элементов из множества  . Следовательно,
. Следовательно,  -линейное многообразие.
-линейное многообразие.
С другой стороны, всякое линейное многообразие, содержащее элементы множества  , содержит и все линейные комбинации элементов из
, содержит и все линейные комбинации элементов из  .
.
Следовательно, линейная оболочка множества  есть наименьшее линейное многообразие, содержащее
есть наименьшее линейное многообразие, содержащее  .
.

 линейного пространства
линейного пространства  называется линейным многообразием, если из
называется линейным многообразием, если из  ,
,  следует, что
следует, что  .
. ; поскольку
; поскольку  , то нулевой элемент принадлежит
, то нулевой элемент принадлежит  ; поскольку
; поскольку  есть элемент, противоположный элементу
есть элемент, противоположный элементу  , то подмножество
, то подмножество  , где
, где  пробегает все числа, образует линейное многообразие.
пробегает все числа, образует линейное многообразие.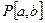 образует линейное многообразие в линейном пространстве непрерывных функций.
образует линейное многообразие в линейном пространстве непрерывных функций. является линейным многообразием в линейном пространстве ограниченных последовательностей.
является линейным многообразием в линейном пространстве ограниченных последовательностей. .
. принадлежат
принадлежат  ,
,  ,
,  .
. ,
, 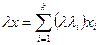 ,
,


