Примеры линейных нормированных пространств
Приведем примеры наиболее часто встречающихся нормированных пространств. При этом первые две аксиомы, как правило, проверяются без труда. Для проверки неравенства треугольника в ряде случаев используются известные неравенства. 1.В арифметическом пространстве
Мы снабдили норму индексом в связи с тем, что в этом же линейном пространстве Проверим аксиомы нормы. 1. 2. Из равенства 3. Имеем
2.В пространстве
Проверим лишь третью аксиому:
Это нормированное пространство обозначается как 3.В пространстве
Неравенство треугольника запишется в виде
Неравенство (2.6) называется неравенством Минковского. Доказательство этого неравенства здесь не приводим, его можно найти в [3,4,5,12]. 4. Рассмотрим множество
Аксиома треугольника сводится к неравенству Минковского для бесконечных сумм
Очевидно, что если 5. Рассмотрим пространство
Проверим неравенство треугольника. Имеем
Отсюда, переходя в левой части к
6. Рассмотрим линейное пространство
Проверим аксиому треугольника. Имеем
Так как неравенство (2.7) справедливо при всех
7. В линейном пространстве
Предлагаем самостоятельно проверить аксиомы нормы. 8. Рассмотрим множество
где Норму в этом множестве определим по формуле
Норма, как легко проверить, не зависит от выбора представителя из класса эквивалентных между собой функций. Неравенство треугольника проверяется с помощью неравенства Минковского для интегралов [3,4,5].
|

 упорядоченных наборов из
упорядоченных наборов из  действительных чисел
действительных чисел  определим норму по формуле
определим норму по формуле .
. - это очевидно. И если
- это очевидно. И если  , т.е.
, т.е.  , то все
, то все  и
и  . Здесь справедливо обратное: норма нулевого элемента равна нулю.
. Здесь справедливо обратное: норма нулевого элемента равна нулю. вытекает однородность нормы.
вытекает однородность нормы. , т.е.
, т.е. . Переходя в этом неравенстве слева к
. Переходя в этом неравенстве слева к  по
по  , получим неравенство треугольника. Это нормированное пространство обозначим как
, получим неравенство треугольника. Это нормированное пространство обозначим как  .
. .
.
 .
. .
. .
. . (2.6)
. (2.6) ,
,  всех числовых последовательностей
всех числовых последовательностей  таких, что числовой ряд
таких, что числовой ряд  сходится. Норму здесь введем по формуле
сходится. Норму здесь введем по формуле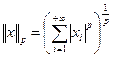 .
. .
.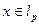 , то и
, то и  для любого числа
для любого числа  . Если же
. Если же 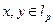 , то как следует из неравенства Минковского
, то как следует из неравенства Минковского  . Итак,
. Итак,  всех ограниченных числовых последовательностей
всех ограниченных числовых последовательностей  . Последовательность
. Последовательность  ограничена, если найдется такое число
ограничена, если найдется такое число  , что верно неравенство
, что верно неравенство  для всех
для всех  .
. .
. , получим
, получим .
. всех непрерывных действительных функций
всех непрерывных действительных функций  , определенных на отрезке
, определенных на отрезке  , и введем норму по формуле
, и введем норму по формуле .
.
 . (2.7)
. (2.7) , то получим
, то получим . Следовательно
. Следовательно  раз непрерывно дифференцируемых на отрезке
раз непрерывно дифференцируемых на отрезке  .
. всех измеримых по Лебегу на отрезке
всех измеримых по Лебегу на отрезке  ,
, - некоторое положительное число. При этом две функции, равные почти всюду, т.е. всюду за исключением множества меры нуль, отождествляются. Иначе говоря, рассматриваются классы эквивалентных между собой функций.
- некоторое положительное число. При этом две функции, равные почти всюду, т.е. всюду за исключением множества меры нуль, отождествляются. Иначе говоря, рассматриваются классы эквивалентных между собой функций. .
.


