Конечномерные нормированные пространства
Имеет место теорема. Теорема 2. Во всяком конечномерном линейном пространстве все нормы эквивалентны. Доказательство. Пусть задано
и введем норму
С этой нормой пространство Пусть
Следовательно, норма
Из неравенства
следует, что
Таким образом, Используя эту теорему, докажем ряд важных предложений. Предложение 15. Для любого
где С – константа, зависящая только от выбора базиса в Доказательство. Из теоремы 2 непосредственно выводим
где Предложение доказано. Предложение 16. В конечномерном нормированном пространстве сходимость по норме совпадает со сходимостью по координатам. Доказательство. Пусть задана последовательность
Вначале предположим, что имеется сходимость по координатам, т.е.
Используя непрерывность суммы и произведения в нормированных пространствах, получим
И доказана сходимость по норме. Теперь предположим, что имеется сходимость по норме. Применяя неравенство (2.12) к элементам
Как следствие этого неравенства: из сходимости по норме следует сходимость по всем координатам. Предложение доказано. Определение 15. Последовательность Нетрудно показать, что любая сходящаяся последовательность фундаментальна. Обратное утверждение, вообще говоря, неверно. Определение 16. Линейное нормированное пространство называется полным, если каждая фундаментальная последовательность имеет предел. Предложение 17. Конечномерное нормированное пространство полно. Доказательство. Возьмем фундаментальную последовательность
Тогда, благодаря полноте множества вещественных чисел существуют конечные пределы
И по предложению 16 имеем
Предложение доказано. Определение 17. Замкнутое линейное многообразие Предложение 18. Всякое конечномерное линейное многообразие Доказательство. Пусть
|

 - мерное линейное пространство
- мерное линейное пространство 
 с базисом
с базисом  . Разложим произвольный элемент этого пространства по базису
. Разложим произвольный элемент этого пространства по базису
 .
. упорядоченных наборов из
упорядоченных наборов из  .
. - еще одна произвольная норма в
- еще одна произвольная норма в  . (2.11)
. (2.11)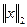 . Далее будем доказывать, что норма
. Далее будем доказывать, что норма  единичного шара
единичного шара  пространства
пространства  .
.

 - непрерывная функция. По теореме Вейерштрасса на ограниченном и замкнутом множестве
- непрерывная функция. По теореме Вейерштрасса на ограниченном и замкнутом множестве  достигает своей нижней грани: найдется
достигает своей нижней грани: найдется  такое, что
такое, что  , где нижняя грань берется по всем
, где нижняя грань берется по всем  . Причем
. Причем 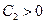 , поскольку
, поскольку  . Отсюда уже для любого
. Отсюда уже для любого  и соответственно для любого
и соответственно для любого  имеем
имеем .
. удовлетворяют неравенству
удовлетворяют неравенству , (2.12)
, (2.12) ,
, , а
, а 
 и элемент
и элемент  ,
,  ,
, .
. ,
,  ,
, .
.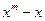 , получим
, получим .
. найдется такой номер
найдется такой номер 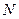 , что для всех
, что для всех  верно неравенство
верно неравенство  .
. ,
,  , получим
, получим .
. ,
,  .
. в нормированном пространстве
в нормированном пространстве  и допустим, что
и допустим, что 
 . Тогда последовательность
. Тогда последовательность  является фундаментальной в
является фундаментальной в  , что
, что  . Но поскольку во всем пространстве
. Но поскольку во всем пространстве  , т.е.
, т.е.  . Это и означает замкнутость линейного многообразия
. Это и означает замкнутость линейного многообразия 


