Определение 13. Пусть в линейном нормированном пространстве  с нормой
с нормой  задана еще одна норма
задана еще одна норма 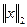 . Говорят, что норма
. Говорят, что норма  подчинена норме
подчинена норме 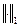 , если найдется такая постоянная
, если найдется такая постоянная  , что
, что
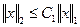 ,
,  . (2.8)
. (2.8)
Имеет место теорема.
Теорема 1. Для сходимости по норме  любой последовательности, сходящейся по норме
любой последовательности, сходящейся по норме 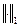 , необходимо и достаточно, чтобы норма
, необходимо и достаточно, чтобы норма  была подчинена норме
была подчинена норме 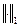 .
.
Доказательство. Достаточность доказывается легко. Действительно, пусть последовательность 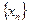 сходится к элементу
сходится к элементу  по первой норме, т.е.
по первой норме, т.е. 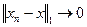 , при
, при 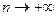 . Тогда из (2.8) имеем
. Тогда из (2.8) имеем
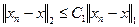 ,
,
откуда следует сходимость последовательности 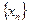 к элементу
к элементу  и по второй норме.
и по второй норме.
Необходимость докажем от противного. Пусть неравенство (2.8) не выполнено. Тогда для любого натурального числа  найдется такой элемент
найдется такой элемент  , что
, что
 .
.
Обе части этого неравенства поделим на одно и то же число  , отличное от нуля, которое затем внесем под знак каждой нормы. В результате получим неравенство
, отличное от нуля, которое затем внесем под знак каждой нормы. В результате получим неравенство

или
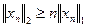 , (2.9)
, (2.9)
где
 ,
,
причем  . С другой стороны из неравенства (2.9) немедленно следует, что
. С другой стороны из неравенства (2.9) немедленно следует, что
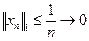 , при
, при 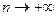 .
.
Таким образом, построили последовательность 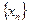 , которая сходится к нулю по первой норме и не сходится по второй. Это противоречие и доказывает теорему.
, которая сходится к нулю по первой норме и не сходится по второй. Это противоречие и доказывает теорему.
Определение 14. Пусть в линейном нормированном пространстве  заданы две нормы:
заданы две нормы:  и
и 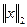 . Нормы
. Нормы  и
и 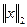 называются эквивалентными, если найдутся такие постоянные
называются эквивалентными, если найдутся такие постоянные  и
и 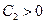 , что
, что
 ,
,  . (2.10)
. (2.10)
Имеет место предложение.
Предложение 14. Две нормы  и
и 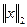 эквивалентны тогда и только тогда, когда сходимость по одной норме влечет сходимость по другой норме.
эквивалентны тогда и только тогда, когда сходимость по одной норме влечет сходимость по другой норме.
Доказательство этого предложения сразу следует из теоремы 1.
В заключение этого параграфа заметим, что отношение эквивалентности норм обладает следующими свойствами:
1. 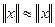 (рефлексивность);
(рефлексивность);
2. Если 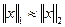 , то
, то  (симметричность);
(симметричность);
3. Если 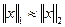 и
и 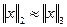 ,то
,то 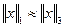 (транзитивность).
(транзитивность).
Здесь значок  означает эквивалентность норм.
означает эквивалентность норм.

 с нормой
с нормой  задана еще одна норма
задана еще одна норма 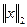 . Говорят, что норма
. Говорят, что норма  подчинена норме
подчинена норме 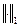 , если найдется такая постоянная
, если найдется такая постоянная  , что
, что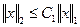 ,
,  . (2.8)
. (2.8)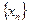 сходится к элементу
сходится к элементу  по первой норме, т.е.
по первой норме, т.е. 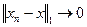 , при
, при 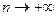 . Тогда из (2.8) имеем
. Тогда из (2.8) имеем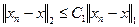 ,
, найдется такой элемент
найдется такой элемент  , что
, что .
. , отличное от нуля, которое затем внесем под знак каждой нормы. В результате получим неравенство
, отличное от нуля, которое затем внесем под знак каждой нормы. В результате получим неравенство
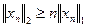 , (2.9)
, (2.9) ,
, . С другой стороны из неравенства (2.9) немедленно следует, что
. С другой стороны из неравенства (2.9) немедленно следует, что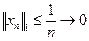 , при
, при 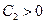 , что
, что ,
,  . (2.10)
. (2.10)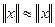 (рефлексивность);
(рефлексивность);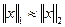 , то
, то  (симметричность);
(симметричность);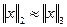 ,то
,то 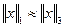 (транзитивность).
(транзитивность). означает эквивалентность норм.
означает эквивалентность норм.


