В нормированных пространствах
Определение 1. Говорят, что в линейном пространстве 1. 2. 3. Предложение 1. Имеет место неравенство
Доказательство. По неравенству треугольника имеем
откуда следует неравенство
Меняя местами в этом неравенстве
Оба последних неравенства в совокупности дают неравенство (2.1). Предложение доказано. Определение 2. В нормированном пространстве
т.е. расстояние между двумя элементами равно норме разности. Предложение 2. Расстояние, определенное формулой (2.2), удовлетворяет аксиомам метрического пространства. Доказательство. Если Далее
Наконец, докажем неравенство треугольника. Используя аксиому 3. для нормы, получим
Предложение доказано. Таким образом, нормированные пространства являются частным случаем метрических пространств. В следующем предложении выражены дополнительные свойства, которыми обладает введенная метрика. Предложение 3. Метрика, определяемая формулой (2.2), удовлетворяет условиям: 1. 2. Доказательство. Имеем
Предложение доказано. Далее справедливо обратное утверждение. Предложение 4. Любая метрика в линейном пространстве, обладающая свойствами (2.3) и (2.4) определяет в некоторую норму, а именно Доказательство. Первая аксиома нормы, очевидно, выполнена. Учитывая положительную однородность метрики, получим
А для доказательства третьей аксиомы воспользуемся неравенством треугольника для метрики и инвариантностью метрики относительно сдвига. Имеем
Предложение доказано. Определение 3. Говорят, что последовательность
Сходимость по норме, очевидно, совпадает со сходимостью по расстоянию, а именно
Имеет место предложение. Предложение 5. Если Доказательство. Из неравенства (2.1) следует
Отсюда непосредственно следует доказательство предложения. Еще отметим, что числовая последовательность Предложение 6. Операции сложения и умножения на число непрерывны в нормированном пространстве: 1) если 2) если Доказательство. Имеем
И первая часть предложения доказана. Для доказательства второго утверждения также используем то, что сходящая числовая последовательность
Предложение доказано.
|

 задана норма, если каждому элементу
задана норма, если каждому элементу  поставлено в соответствие неотрицательное число, обозначаемое как
поставлено в соответствие неотрицательное число, обозначаемое как  , причем должны выполняться три аксиомы:
, причем должны выполняться три аксиомы:
 (невырожденность нормы);
(невырожденность нормы); , каково бы ни было число
, каково бы ни было число  (однородность нормы);
(однородность нормы); (неравенство треугольника).
(неравенство треугольника). . (2.1)
. (2.1) ,
, .
. и
и  , получим
, получим .
.
 , (2.2)
, (2.2) , то
, то  и по аксиоме 1. для нормы
и по аксиоме 1. для нормы  ; если же
; если же  , то
, то  .
. .
.
 .
. (инвариантность относительно сдвига); (2.3)
(инвариантность относительно сдвига); (2.3) (положительная однородность). (2.4)
(положительная однородность). (2.4) ,
, .
. .
. .
. .
. сходится к
сходится к  , если
, если , при
, при 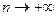 . (2.5)
. (2.5)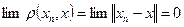 .
. , то
, то  , иначе говоря, норма является непрерывной функцией.
, иначе говоря, норма является непрерывной функцией. .
. ограничена, как сходящаяся.
ограничена, как сходящаяся. , то
, то  ;
; , то
, то  , где
, где  - числа.
- числа.
 .
. ограничена. С учетом этого имеем
ограничена. С учетом этого имеем
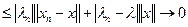 .
.


