Определение 12. Множество 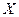 называется упорядоченным, если для некоторых пар элементов
называется упорядоченным, если для некоторых пар элементов  и
и  определено отношение порядка
определено отношение порядка  (
( меньше или равно
меньше или равно  ), причем для любых
), причем для любых 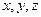 из
из  выполнены условия:
выполнены условия:
1) 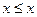 для любого
для любого 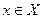 (рефлексивность);
(рефлексивность);
2) если  и
и 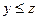 , то
, то 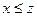 (транзитивность);
(транзитивность);
3) если  и
и 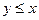 то
то  (антисимметричность).
(антисимметричность).
Определение 13. Упорядоченное множество 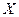 называется совершенно упорядоченным, если для любых элементов
называется совершенно упорядоченным, если для любых элементов  и
и  из
из 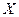 либо
либо  , либо
, либо 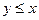 , т.е. все элементы сравнимы между собой.
, т.е. все элементы сравнимы между собой.
Определение 14. Подмножество 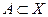 называется ограниченным сверху, если существует такой
называется ограниченным сверху, если существует такой 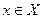 , что
, что 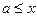 для любого
для любого 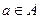 . При этом
. При этом  называется верхней границей для
называется верхней границей для 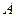 .
.
Определение 15. Если 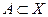 , то элемент
, то элемент 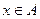 называется наибольшим в
называется наибольшим в 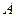 , если
, если 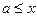 для любого
для любого 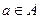 .
.
Определение 16. Если 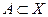 , то элемент
, то элемент 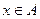 называется максимальным в
называется максимальным в 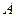 , если из
, если из 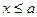 для
для 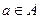 , следует что
, следует что 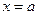 .
.
Отметим, что любой наибольший элемент будет и максимальным, но, вообще говоря, не наоборот.
Лемма Цорна. Если каждое совершенно упорядоченное подмножество упорядоченного множества 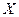 ограничено сверху, то в
ограничено сверху, то в 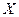 существует максимальный элемент.
существует максимальный элемент.
Далее рассмотрим одно из применений Леммы Цорна в линейных пространствах.
С этой целью введем ряд определений.
Определение 17. Множество 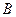 в линейном пространстве
в линейном пространстве  называется линейно независимым, если любой конечный набор
называется линейно независимым, если любой конечный набор 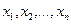 элементов из
элементов из 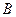 линейно независим.
линейно независим.
Определение 18. Множество 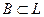 называется алгебраическим базисом пространства
называется алгебраическим базисом пространства  , если
, если 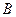 линейно независимо и для любого
линейно независимо и для любого  существует конечный набор
существует конечный набор 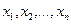 элементов из
элементов из 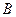 , такой, что
, такой, что 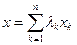 .
.
Теорема 3. В любом линейном пространстве 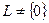 существует алгебраический базис.
существует алгебраический базис.
Доказательство. Обозначим через 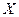 множество всевозможных линейно независимых подмножеств из
множество всевозможных линейно независимых подмножеств из  . На
. На 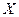 зададим отношение порядка по включению, а именно: если
зададим отношение порядка по включению, а именно: если 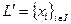 и
и 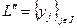 два линейно независимых множества, то будем писать
два линейно независимых множества, то будем писать 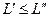 , если
, если 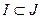 и
и 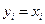 при
при 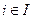 . Таким образом, множество
. Таким образом, множество 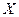 становится частично упорядоченным. Пусть
становится частично упорядоченным. Пусть 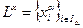 - совершенно упорядоченное подмножество
- совершенно упорядоченное подмножество 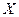 , где
, где 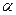 пробегает некоторое множество
пробегает некоторое множество 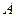 . Покажем, что оно ограничено сверху.
. Покажем, что оно ограничено сверху.
Положим 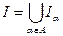 . Если
. Если 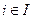 , то
, то 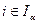 при некотором
при некотором 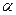 . Далее докажем, что в силу совершенной упорядоченности множества
. Далее докажем, что в силу совершенной упорядоченности множества 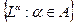 все элементы
все элементы 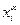 , такие, что
, такие, что 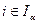 совпадают между собой. В самом деле, если
совпадают между собой. В самом деле, если 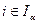 и
и 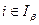 , то либо
, то либо 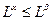 , либо
, либо 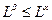 . В первом случае
. В первом случае 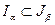 и
и 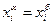 для всех
для всех 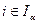 . Аналогичное соотношение имеет место во втором случае.
. Аналогичное соотношение имеет место во втором случае.
Теперь определим элемент 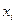 с помощью равенства
с помощью равенства 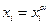 , где
, где 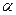 - любой из индексов, для которых
- любой из индексов, для которых 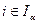 . Тогда множество
. Тогда множество 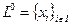 линейно независимо, в силу совершенной упорядоченности
линейно независимо, в силу совершенной упорядоченности 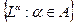 , и является верхней гранью для
, и является верхней гранью для 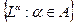 .
.
Значит, выполнены условия леммы Цорна и в 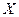 существует максимальное линейно независимое множество
существует максимальное линейно независимое множество 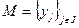 . Нам остается доказать, что множество
. Нам остается доказать, что множество  и есть алгебраический базис. Оно линейно независимо. И если линейная оболочка
и есть алгебраический базис. Оно линейно независимо. И если линейная оболочка  не совпадает со всем пространством
не совпадает со всем пространством  , то найдется ненулевой элемент
, то найдется ненулевой элемент 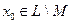 . Присоединяя элемент
. Присоединяя элемент 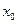 к множеству
к множеству  , мы получим такое линейно независимое множество
, мы получим такое линейно независимое множество  , что
, что 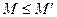 . А это противоречит максимальности
. А это противоречит максимальности  . Теорема полностью доказана.
. Теорема полностью доказана.

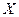 называется упорядоченным, если для некоторых пар элементов
называется упорядоченным, если для некоторых пар элементов  и
и  определено отношение порядка
определено отношение порядка  (
(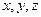 из
из 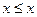 для любого
для любого 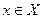 (рефлексивность);
(рефлексивность);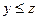 , то
, то 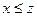 (транзитивность);
(транзитивность);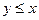 то
то  (антисимметричность).
(антисимметричность).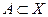 называется ограниченным сверху, если существует такой
называется ограниченным сверху, если существует такой 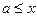 для любого
для любого 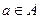 . При этом
. При этом 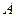 .
.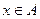 называется наибольшим в
называется наибольшим в 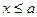 для
для 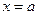 .
.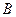 в линейном пространстве
в линейном пространстве  называется линейно независимым, если любой конечный набор
называется линейно независимым, если любой конечный набор 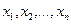 элементов из
элементов из 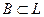 называется алгебраическим базисом пространства
называется алгебраическим базисом пространства  существует конечный набор
существует конечный набор 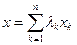 .
.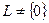 существует алгебраический базис.
существует алгебраический базис.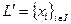 и
и 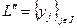 два линейно независимых множества, то будем писать
два линейно независимых множества, то будем писать 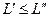 , если
, если 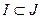 и
и 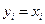 при
при 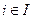 . Таким образом, множество
. Таким образом, множество 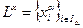 - совершенно упорядоченное подмножество
- совершенно упорядоченное подмножество 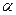 пробегает некоторое множество
пробегает некоторое множество 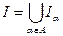 . Если
. Если 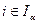 при некотором
при некотором 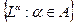 все элементы
все элементы 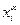 , такие, что
, такие, что 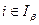 , то либо
, то либо 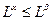 , либо
, либо 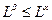 . В первом случае
. В первом случае 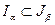 и
и 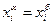 для всех
для всех 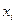 с помощью равенства
с помощью равенства 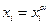 , где
, где 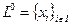 линейно независимо, в силу совершенной упорядоченности
линейно независимо, в силу совершенной упорядоченности 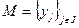 . Нам остается доказать, что множество
. Нам остается доказать, что множество  и есть алгебраический базис. Оно линейно независимо. И если линейная оболочка
и есть алгебраический базис. Оно линейно независимо. И если линейная оболочка 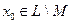 . Присоединяя элемент
. Присоединяя элемент 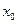 к множеству
к множеству  , что
, что 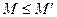 . А это противоречит максимальности
. А это противоречит максимальности 


