В пособии [12] подробно изложены компактные пространства и множества в метрических пространствах. Здесь рассмотрим один аспект, характерный именно для линейных нормированных пространств. В начале приведем нужные определения.
Определение 1. Линейное нормированное пространство  называется компактным, если у любой последовательности точек этого пространства существует сходящаяся подпоследовательность.
называется компактным, если у любой последовательности точек этого пространства существует сходящаяся подпоследовательность.
Определение 2. Линейное нормированное пространство  называется относительно компактным, если у любой последовательности точек этого пространства существует фундаментальная подпоследовательность.
называется относительно компактным, если у любой последовательности точек этого пространства существует фундаментальная подпоследовательность.
Определение 3. Множество  в линейном нормированном пространство
в линейном нормированном пространство  называется относительно компактным, если у любой последовательности точек этого множества существует фундаментальная подпоследовательность.
называется относительно компактным, если у любой последовательности точек этого множества существует фундаментальная подпоследовательность.
Определение 3. Неограниченное множество 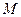 элементов нормированного пространства
элементов нормированного пространства  называется локально относительно компактным, если пересечение
называется локально относительно компактным, если пересечение 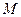 с любым замкнутым шаром в
с любым замкнутым шаром в  относительно компактно.
относительно компактно.
Теорема 1. (Ф.Рисс). Для того чтобы линейное многообразие  нормированного пространства
нормированного пространства  было локально относительно компактным, необходимо и достаточно, чтобы
было локально относительно компактным, необходимо и достаточно, чтобы  было конечномерным.
было конечномерным.
Доказательство необходимости. Пусть  локально компактно. Рассмотрим точку
локально компактно. Рассмотрим точку  и произвольный замкнутый шар
и произвольный замкнутый шар  с центром в этой точке
с центром в этой точке  . Пересечение
. Пересечение  относительно компактно в
относительно компактно в  .
.
Предположим, что утверждение теоремыневерно, т.е.  бесконечномерно.
бесконечномерно.
Возьмем любой элемент  с
с  и положим
и положим  . Обозначим через
. Обозначим через 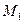 линейную оболочку элемента
линейную оболочку элемента  , т.е. множество элементов вида
, т.е. множество элементов вида  .
.
По лемме Рисса существует 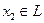 с
с  такой, что
такой, что  и, в частности,
и, в частности,  . Положим
. Положим  . Тогда
. Тогда  и, кроме того,
и, кроме того,
 .
.
Продолжим эти построения. Если  и, соответственно
и, соответственно  ,
,  , уже построены, то через
, уже построены, то через  обозначим линейную оболочку элементов
обозначим линейную оболочку элементов  .
.
Линейное многообразие  замкнуто, поскольку конечномерно, т.е. является подпространством. Так как
замкнуто, поскольку конечномерно, т.е. является подпространством. Так как  бесконечномерно, то
бесконечномерно, то 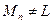 . Снова пользуясь леммой Рисса, найдем элемент
. Снова пользуясь леммой Рисса, найдем элемент  с
с  такой, что
такой, что  . В частности,
. В частности,  при любом
при любом  . Положим
. Положим  . Тогда
. Тогда  и выполнено неравенство
и выполнено неравенство
 ,
,  . (2.15)
. (2.15)
Продолжая этот процесс, получим последовательность  , которая не содержит фундаментальной последовательности. А это противоречит относительной компактности
, которая не содержит фундаментальной последовательности. А это противоречит относительной компактности  . Необходимость доказана.
. Необходимость доказана.
Доказательство достаточности. Пусть  конечномерно. Возьмем в
конечномерно. Возьмем в  произвольный замкнутый шар
произвольный замкнутый шар  . Рассмотрим в ограниченном множестве
. Рассмотрим в ограниченном множестве  произвольную последовательность
произвольную последовательность  . Разложим элементы этой последовательности по базису
. Разложим элементы этой последовательности по базису  ,
,  . На основании предложения 15 из 2-ой главы заключаем, что при каждом
. На основании предложения 15 из 2-ой главы заключаем, что при каждом  числовая последовательность
числовая последовательность  ограничена. Поэтому по известной теореме Больцано - Вейерштрасса существует последовательность натуральных чисел
ограничена. Поэтому по известной теореме Больцано - Вейерштрасса существует последовательность натуральных чисел  такая, что
такая, что
 ,
,  .
.
Тогда в силу предложения16 из 2-ой главы
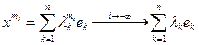 .
.
Это и означает, что  относительно компактно. Теорема полностью доказана.
относительно компактно. Теорема полностью доказана.
Следствие 1. Для того, чтобы нормированное пространство было локально компактным, необходимо и достаточно, чтобы оно было конечномерным.
Доказательство получается из теоремы, если взять  .
.
Следствие 2. В бесконечномерном нормированном пространстве любое относительно компактное множество нигде не плотно.
Доказательство. Пусть 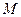 - относительно компактное множество в бесконечномерном пространстве
- относительно компактное множество в бесконечномерном пространстве  . Допустим, что утверждение следствия неверно. Тогда найдется шар
. Допустим, что утверждение следствия неверно. Тогда найдется шар  , который содержится в замыкании множества
, который содержится в замыкании множества 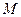 :
:  . Но тогда
. Но тогда  . Поскольку
. Поскольку 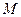 - относительно компактно, то относительно компактными будут также множества
- относительно компактно, то относительно компактными будут также множества 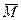 и
и  . Из относительной компактности
. Из относительной компактности  по следствию 1 получаем, что
по следствию 1 получаем, что  - конечномерно. Полученное противоречие и доказывает следствие.
- конечномерно. Полученное противоречие и доказывает следствие.

 называется компактным, если у любой последовательности точек этого пространства существует сходящаяся подпоследовательность.
называется компактным, если у любой последовательности точек этого пространства существует сходящаяся подпоследовательность. в линейном нормированном пространство
в линейном нормированном пространство 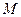 элементов нормированного пространства
элементов нормированного пространства  нормированного пространства
нормированного пространства  и произвольный замкнутый шар
и произвольный замкнутый шар  с центром в этой точке
с центром в этой точке  относительно компактно в
относительно компактно в  с
с  и положим
и положим  . Обозначим через
. Обозначим через 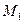 линейную оболочку элемента
линейную оболочку элемента  , т.е. множество элементов вида
, т.е. множество элементов вида  .
.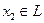 с
с  и, в частности,
и, в частности,  . Положим
. Положим  . Тогда
. Тогда  и, кроме того,
и, кроме того, .
. и, соответственно
и, соответственно  ,
,  , уже построены, то через
, уже построены, то через  обозначим линейную оболочку элементов
обозначим линейную оболочку элементов 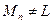 . Снова пользуясь леммой Рисса, найдем элемент
. Снова пользуясь леммой Рисса, найдем элемент  с
с  такой, что
такой, что  . В частности,
. В частности,  при любом
при любом  . Положим
. Положим  . Тогда
. Тогда  и выполнено неравенство
и выполнено неравенство ,
,  , которая не содержит фундаментальной последовательности. А это противоречит относительной компактности
, которая не содержит фундаментальной последовательности. А это противоречит относительной компактности  . Рассмотрим в ограниченном множестве
. Рассмотрим в ограниченном множестве  . Разложим элементы этой последовательности по базису
. Разложим элементы этой последовательности по базису  ,
,  . На основании предложения 15 из 2-ой главы заключаем, что при каждом
. На основании предложения 15 из 2-ой главы заключаем, что при каждом  ограничена. Поэтому по известной теореме Больцано - Вейерштрасса существует последовательность натуральных чисел
ограничена. Поэтому по известной теореме Больцано - Вейерштрасса существует последовательность натуральных чисел  такая, что
такая, что ,
, 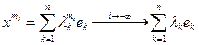 .
. .
. , который содержится в замыкании множества
, который содержится в замыкании множества  . Но тогда
. Но тогда  . Поскольку
. Поскольку 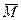 и
и  . Из относительной компактности
. Из относительной компактности 


