Определение 1. Последовательность 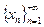 элементов нормированного пространства называется фундаментальной, если для любого положительного числа
элементов нормированного пространства называется фундаментальной, если для любого положительного числа  найдется такой номер
найдется такой номер 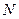 , что для всех
, что для всех 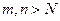 верно неравенство
верно неравенство 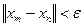 .
.
Предложение 1. Если последовательность 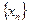 сходится к пределу
сходится к пределу  , то она является фундаментальной или последовательностью Коши.
, то она является фундаментальной или последовательностью Коши.
Доказательство. Пусть  . Тогда для любого
. Тогда для любого 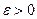 найдется номер
найдется номер 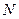 такой, что
такой, что 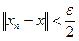 при
при 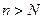 . Следовательно,
. Следовательно,
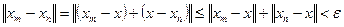
для всех 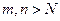 . Предложение доказано.
. Предложение доказано.
Нетрудно показать, что любая сходящаяся последовательность фундаментальна. Обратное утверждение, вообще говоря, неверно.
Определение 2. Линейное нормированное пространство называется полным, если каждая фундаментальная последовательность имеет предел.
Полные нормированные пространства называют банаховыми пространствами.
Теорема 1. Для любого линейного нормированного пространства  существует банахово пространство
существует банахово пространство 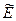 такое, что
такое, что
1. 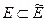 ;
;
2. 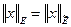 ,
, 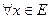 ;
;
3.  всюду плотно в
всюду плотно в 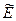 , т.е.
, т.е.  .
.
Доказательство разобьем на несколько этапов.
I. Две фундаментальные последовательности 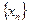 и
и 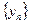 элементов
элементов  назовем
назовем
эквивалентными (и запишем 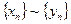 ), если
), если
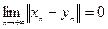 .
.
Введенное отношение, как легко заметить, рефлексивно и симметрично. Докажем, что оно также транзитивно. Пусть 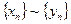 и
и 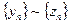 , т.е.
, т.е. 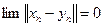 и
и 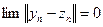 . Тогда в силу неравенства треугольника
. Тогда в силу неравенства треугольника
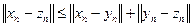 ,
,
откуда 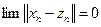 , т.е.
, т.е. 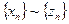 .
.
Следовательно, множество всех фундаментальных последовательностей из элементов  распадается на классы эквивалентных последовательностей. Множество этих классов обозначим через
распадается на классы эквивалентных последовательностей. Множество этих классов обозначим через 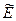 и докажем, что оно является искомым банаховым пространством.
и докажем, что оно является искомым банаховым пространством.
II. Определим в множестве 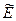 операции сложения и умножения на число. Пусть
операции сложения и умножения на число. Пусть 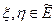 и пусть
и пусть 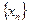 и
и 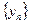 - некоторые последовательности из этих классов. Поскольку
- некоторые последовательности из этих классов. Поскольку 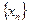 ,
, 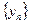 - фундаментальные последовательности, то и последовательность
- фундаментальные последовательности, то и последовательность 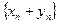 также является фундаментальной. Поэтому она входит в некоторый класс, который обозначим через
также является фундаментальной. Поэтому она входит в некоторый класс, который обозначим через 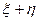 . Покажем независимость от выбора представителей классов
. Покажем независимость от выбора представителей классов 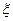
и 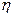 . Пусть
. Пусть  ,
, 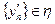 . Тогда по определению классов
. Тогда по определению классов  и
и 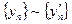 . Это означает, что
. Это означает, что
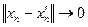 ,
, 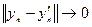 , когда
, когда 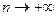 .
.
Используя неравенство треугольника, получим
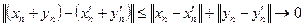 , когда
, когда 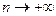 ,
,
поэтому  , т.е.
, т.е. 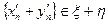 , что и доказывает корректность операции сложения.
, что и доказывает корректность операции сложения.
Далее определим умножение на число. Вместе с последовательностью 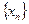 фундаментальной будет, очевидно, и последовательность
фундаментальной будет, очевидно, и последовательность 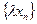 . Поэтому
. Поэтому 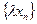 принадлежит некоторому классу, который мы обозначим через
принадлежит некоторому классу, который мы обозначим через 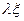 . Проверим корректность определения. Если
. Проверим корректность определения. Если 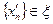 , то
, то 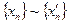 , т.е.
, т.е. 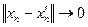 , поэтому и
, поэтому и 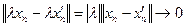 , т.е.
, т.е. 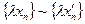 . Следовательно
. Следовательно  .
.
Таким образом 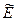 - линейное пространство. В заключение этого пункта определим, какой элемент играет роль нулевого элемента
- линейное пространство. В заключение этого пункта определим, какой элемент играет роль нулевого элемента 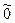 в
в 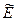 . Этот элемент определяется условием
. Этот элемент определяется условием  ,
, 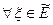 . Возьмем
. Возьмем 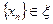 , тогда получим, что класс
, тогда получим, что класс 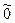 содержит стационарную последовательность
содержит стационарную последовательность  .
.
III. Введем в 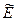 норму. Для заданного класса
норму. Для заданного класса 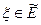 выберем представителя
выберем представителя 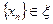 . Из неравенства
. Из неравенства
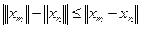
и фундаментальности последовательности 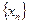 следует фундаментальность числовой последовательности
следует фундаментальность числовой последовательности  . Положим по определению
. Положим по определению
 . (3.1)
. (3.1)
И если имеется другой представитель 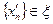 , то
, то
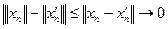 , когда
, когда 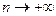 ,
,
и поэтому норма не зависит от выбора последовательности.
Далее проверим аксиомы нормы, определенной по формуле (3.1). Очевидно, 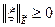 и, если
и, если 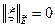 ,то
,то
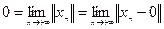 ,
,
т.е. 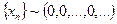 . Таким образом класс
. Таким образом класс  содержит стационарную последовательность
содержит стационарную последовательность  , т.е.
, т.е. 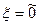 . Теперь переходя к пределу в соотношениях
. Теперь переходя к пределу в соотношениях
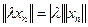 ,
,
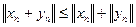 ,
,
получим вторую и третью аксиомы нормы
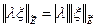 ,
,
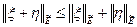 .
.
IV. Покажем, что пространство  можно рассмотреть как часть
можно рассмотреть как часть 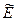 . Для этого каждому элементу
. Для этого каждому элементу 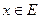 поставим в соответствие тот класс
поставим в соответствие тот класс 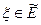 , который состоит из последовательностей, сходящихся к элементу
, который состоит из последовательностей, сходящихся к элементу  . Он не пуст, поскольку содержит стационарную последовательность
. Он не пуст, поскольку содержит стационарную последовательность 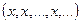 . И, согласно формуле (3.1),
. И, согласно формуле (3.1),
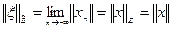 .
.
Множество всех классов, содержащих стационарные последовательности, является линейным многообразием в 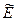 . Для этого линейного многообразия сохраним обозначение
. Для этого линейного многообразия сохраним обозначение  .
.
V. Докажем, что  всюду плотно в
всюду плотно в 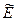 . Возьмем любой класс
. Возьмем любой класс 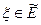 и произвольное число
и произвольное число 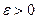 . Необходимо показать, что в шаре
. Необходимо показать, что в шаре 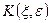 с центром в
с центром в  и радиуса
и радиуса 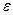 найдется хоть одна точка из
найдется хоть одна точка из  . Возьмем некоторую последовательность
. Возьмем некоторую последовательность 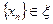 . Поскольку она фундаментальна, то найдется такое
. Поскольку она фундаментальна, то найдется такое  , что при
, что при 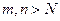 верно неравенство
верно неравенство
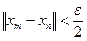 .
.
Введем в рассмотрение стационарную последовательность 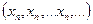 . Тогда при
. Тогда при 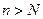 имеем
имеем
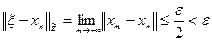 , (3.2)
, (3.2)
т.е. 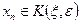 при всех
при всех 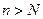 .
.
Неравенство (3.2) еще означает, что  , как элемент пространства
, как элемент пространства 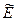 сходится к
сходится к  :
: 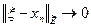 , при
, при 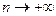 .
.
VI. Наконец, докажем полноту 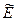 . Пусть дана последовательность
. Пусть дана последовательность 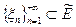 . Поскольку
. Поскольку  плотно в
плотно в 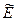 , то для каждого
, то для каждого 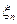 можно найти
можно найти 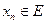 такой, что
такой, что
 ,
, 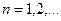 .
.
В результате получим последовательность  . Покажем, что она фундаментальна. В самом деле,
. Покажем, что она фундаментальна. В самом деле,
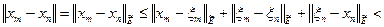
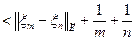 ,
,
и фундаментальность  следует из фундаментальности
следует из фундаментальности  . Обозначим через
. Обозначим через  класс, содержащий последовательность
класс, содержащий последовательность 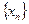 . Как отмечено в конце предыдущего пункта
. Как отмечено в конце предыдущего пункта
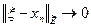 , при
, при 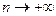 .
.
Отсюда и из неравенства треугольника следует
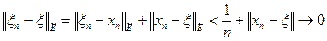 , когда
, когда 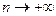 .
.
Таким образом, последовательность  сходится к элементу
сходится к элементу  . Теорема полностью доказана.
. Теорема полностью доказана.

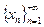 элементов нормированного пространства называется фундаментальной, если для любого положительного числа
элементов нормированного пространства называется фундаментальной, если для любого положительного числа  найдется такой номер
найдется такой номер 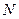 , что для всех
, что для всех 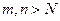 верно неравенство
верно неравенство 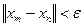 .
.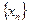 сходится к пределу
сходится к пределу  , то она является фундаментальной или последовательностью Коши.
, то она является фундаментальной или последовательностью Коши. . Тогда для любого
. Тогда для любого 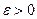 найдется номер
найдется номер 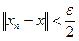 при
при 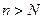 . Следовательно,
. Следовательно,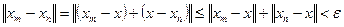
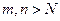 . Предложение доказано.
. Предложение доказано. существует банахово пространство
существует банахово пространство 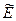 такое, что
такое, что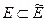 ;
;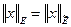 ,
, 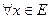 ;
; .
.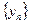 элементов
элементов 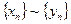 ), если
), если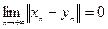 .
.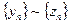 , т.е.
, т.е. 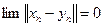 и
и 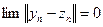 . Тогда в силу неравенства треугольника
. Тогда в силу неравенства треугольника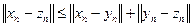 ,
,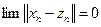 , т.е.
, т.е. 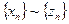 .
.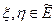 и пусть
и пусть 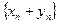 также является фундаментальной. Поэтому она входит в некоторый класс, который обозначим через
также является фундаментальной. Поэтому она входит в некоторый класс, который обозначим через 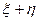 . Покажем независимость от выбора представителей классов
. Покажем независимость от выбора представителей классов 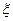
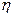 . Пусть
. Пусть  ,
, 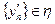 . Тогда по определению классов
. Тогда по определению классов  и
и 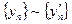 . Это означает, что
. Это означает, что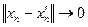 ,
, 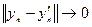 , когда
, когда 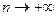 .
.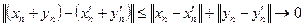 , когда
, когда 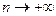 ,
, , т.е.
, т.е. 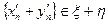 , что и доказывает корректность операции сложения.
, что и доказывает корректность операции сложения.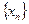 фундаментальной будет, очевидно, и последовательность
фундаментальной будет, очевидно, и последовательность 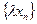 . Поэтому
. Поэтому 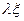 . Проверим корректность определения. Если
. Проверим корректность определения. Если 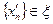 , то
, то 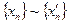 , т.е.
, т.е. 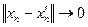 , поэтому и
, поэтому и 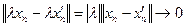 , т.е.
, т.е. 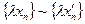 . Следовательно
. Следовательно  .
.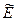 - линейное пространство. В заключение этого пункта определим, какой элемент играет роль нулевого элемента
- линейное пространство. В заключение этого пункта определим, какой элемент играет роль нулевого элемента 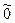 в
в  ,
, 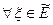 . Возьмем
. Возьмем 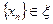 , тогда получим, что класс
, тогда получим, что класс  .
.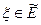 выберем представителя
выберем представителя 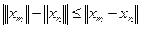
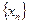 следует фундаментальность числовой последовательности
следует фундаментальность числовой последовательности  . Положим по определению
. Положим по определению . (3.1)
. (3.1)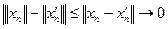 , когда
, когда 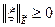 и, если
и, если 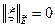 ,то
,то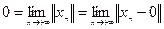 ,
,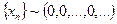 . Таким образом класс
. Таким образом класс  содержит стационарную последовательность
содержит стационарную последовательность 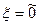 . Теперь переходя к пределу в соотношениях
. Теперь переходя к пределу в соотношениях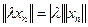 ,
,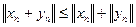 ,
,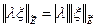 ,
,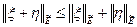 .
. можно рассмотреть как часть
можно рассмотреть как часть 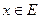 поставим в соответствие тот класс
поставим в соответствие тот класс  . Он не пуст, поскольку содержит стационарную последовательность
. Он не пуст, поскольку содержит стационарную последовательность 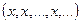 . И, согласно формуле (3.1),
. И, согласно формуле (3.1),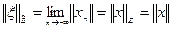 .
.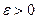 . Необходимо показать, что в шаре
. Необходимо показать, что в шаре 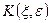 с центром в
с центром в 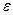 найдется хоть одна точка из
найдется хоть одна точка из  , что при
, что при 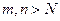 верно неравенство
верно неравенство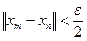 .
.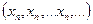 . Тогда при
. Тогда при 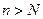 имеем
имеем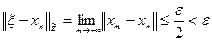 , (3.2)
, (3.2)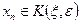 при всех
при всех  , как элемент пространства
, как элемент пространства 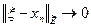 , при
, при 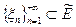 . Поскольку
. Поскольку 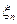 можно найти
можно найти 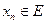 такой, что
такой, что ,
, 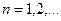 .
. . Покажем, что она фундаментальна. В самом деле,
. Покажем, что она фундаментальна. В самом деле,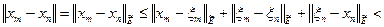
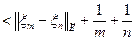 ,
, . Обозначим через
. Обозначим через 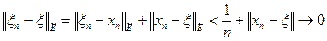 , когда
, когда 


