ЛИНЕЙНЫЕ ПРОСТРАНСТВА
1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.:Наука,1972.496с. 2. Канторович Л. В., Акилов Г.П. Функциональный анализ. М.:Наука,1977. 742с. 3. Люстерник Л.А., Соболев В.И. Элементы функционального анализа. М.: Наука,1965. 520с. 4. Антоневич А.Б., Радыно Я.В. Функциональный анализ и интегральные уравнения. Мн.: БГУ,2003.430с. 5.Треногин В.А. Функциональный анализ. М.:Наука,1980.496с. 6. Морен К. Методы гильбертова пространства. М.:Мир,1965.572с. 7. Треногин В.А., Писаревский Б.М., Соболева Т.С. Задачи и упражнения по функциональному анализу. М.:Физматлит,2002.240с. 8. Городецкий В.В., Нагнибеда Н.И., Настиев П.П. Методы решения задач по функциональному анализу. Киев:Вища шк.1990.479с. 9. Петров В.А., Виленкин Н.Я., Граев М.И. Элементы функционального анализа в задачах. М.Просвещение,1978.128с.
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ Часть 2. Нормированные пространства. Теория и задачи с решениями.
Учебно-методическое пособие
ВЕЛИКИЙ НОВГОРОД
УДК 517.5 Печатается по решению РИС НовГУ
Рецензент Кандидат физико-математических наук, доцент О.Н. Барсов
Функциональный анализ. Часть 2. Нормированные пространства. Теория и задачи с решениями.: учеб. - метод. пособие / Сост.: С.И. Эминов; НовГУ им. Ярослава Мудрого. - Великий Новгород, 2007. – 64 с.
Излагаются основы нормированных пространств, а также приводятся задачи с решениями. Предназначено для студентов и аспирантов математических, физических и инженерных специальностей, а также для научных работников.
УДК 517.5
© Новгородский государственный университет, 2008 © С.И. Эминов, составление, 2008
Посвящается моим одноклассникам, окончившим Тбилисскую физико-математическую школу-интернат имени Комарова в 1976 г., учащимся ныне живущим в Австралии, Армении, Греции, Грузии, Израиле, Канаде, Панаме, России, США, Украине и Швейцарии.
ОГЛАВЛЕНИЕ ПРЕДИСЛОВИЕ……………………………………………………………...........................5 1.ЛИНЕЙНЫЕ ПРОСТРАНСТВА…………………...…………………..............................6 1.1. Аксиомы линейного пространства и простейшие следствия……...………………….6 1.2. Примеры линейных пространств………………………………………………………..8 1.3. Размерность. Базис конечномерного пространства…………………………………....9 1.4. Линейное многообразие. Линейные оболочки………………….…………………….11 1.5. Изоморфизм линейных пространств……………………………………………….….13 1.6. Фактор - пространства……………………………………………………………….....13 1.7. Прямые суммы………………………………………………………………………….14
2. НОРМИРОВАННЫЕ ПРОСТРАНСТВА……………………………………………....17 2.1.Определение нормированного пространства, связь с метрическими пространствами. Непрерывность операций сложения и умножения на число в нормированных пространствах…………………17 2.2. Примеры линейных нормированных пространств…………………………………...20 2.3. Открытые и замкнутые множества. Точки прикосновения и предельные точки…………………………………………...23 2.4. Эквивалентные нормы……………………………………………….………………....25 2.5. Конечномерные нормированные пространства………………………………………27 2.6. Расстояние от точки до подпространства. Приближение элементами подпространства………………………………………….30 2.7. Лемма Рисса. Об одном применении леммы Рисса…………………………………. 32 2.8. Компактность и конечномерность…………………………………………………….34 3. БАНАХОВЫ ПРОСТРАНСТВА………………………………………………………..36 3.1. Пополнение нормированного пространства………………….. ……………………..36 3.2. Ряды в нормированных и банаховых пространствах…..…………………………….40 3.3. Принцип вложенных шаров. Множества первой и второй категории……………...42 3.4. Фактор - пространства нормированных пространств………...……………………...43 3.5. Банахово пространство с базисом……………………………………...……………...44 4. ЗАДАЧИ……….…………………………………………………………………………..46 5. РЕШЕНИЯ……………………………………….………………………………………..50 ЛИТЕРАТУРА……………………………………………………………………………….63
ПРЕДИСЛОВИЕ Линейные нормированные пространства представляют чрезвычайно важный раздел функционального анализа. В учебниках по функциональному анализу нормированные пространства излагаются, как правило, крайне лаконично и трудно доступно для самостоятельного изучения. Кроме того, многие учебники в настоящее время становятся библиографической редкостью. В этой связи представляется актуальным разработка методического пособия, что позволило бы частично восполнить имеющийся пробел. Пособие состоит из трех глав. В первой главе приводятся основные сведения о линейных пространствах. В конце этой главы формулируется лемма Цорна и приводится одно из применений указанной леммы. Вторая глава посвящена нормированным пространствам. Здесь подробно доказываются основные теоремы нормированных пространств. Наряду с бесконечномерными пространствами обстоятельно изучаются конечномерные нормированные пространства. В третьей главе изучается важный класс нормированных пространств – банаховы пространства. В этой главе доказывается теорема о пополнении произвольного линейного нормированного пространства, затем излагаются основные свойства банаховых пространств. Наряду с теорией в пособии приведены задачи с решениями. По замыслу, теория и задачи с решениями должны представить в определенной полноте методы и приемы, характерные для нормированных пространств. Мы рекомендуем студентам вначале самостоятельно решить задачу, используя методы и приемы, развиваемые при доказательствах теорем. И лишь затем сравнить свое решение с решением, которое приводится в пособии. Пособие предназначено как студентам, так и аспирантам и научным работникам, желающим основательно проработать нормированные пространства. Во время работы над пособием, я обсуждал некоторые вопросы с профессорами Захаровым Анатолием Юрьевичем и Пановым Евгением Юрьевичем. Я выражаю им свою искреннюю благодарность.
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
|

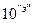 класса,
класса, .Лемма Цорна. Существование алгебраического базиса…………………………….15
.Лемма Цорна. Существование алгебраического базиса…………………………….15


