Экранирование зарядов в плазме. Дебаевский радиус
Важной характеристикой плазмы является величина, называемая длиной экранирования, или дебаевским радиусом. Каждая заряженная частица вызывает поляризацию плазмы, т.е. накопление вокруг нее частиц противоположного знака, что и приводит к экранированию поля частицы. Экранированный потенциал может быть вычислен с помощью теории Дебая, развитой в начале 20-го столетия для растворов электролитов. Для упрощения задачи будем использовать следующие предположения: а) плазма является изотермической, а частицы в ней распределены по закону Больцмана; б) положительные ионы являются однозарядными; в) плазма является безграничной; г) можно пренебречь микрофлуктуациями потенциала, связанными с дискретностью зарядов. Будем рассуждать следующим образом. Положительно заряженный ион создает вокруг себя электрическое поле с потенциалом
где
где qi = е – заряд иона. При Из (13) и (14) вытекает, что объемная плотность зарядов в плазме равна
где
или
Уравнение (17) – нелинейное, и построить его решение удается только после линеаризации, т.е. в приближении
Тогда, принимая во внимание известное соотношение
где величина
называется радиусом экранирования или дебаевским радиусом. Для решения уравнения (19) воспользуемся известным из теории обобщенных функций соотношением
и его следствием
Тогда решение уравнения (19) можно представить в виде
при условии, что А + В =1. Коэффициент В должен равняться 0, иначе потенциал
Построенный потенциал
Это означает, что в месте расположения иона создается потенциал
который определяет потенциальную энергию этого поля в плазме:
такое же значение энергии получается и для электрона. Если потенциальная энергия электронов ионов плазмы много меньше (по модулю) их кинетической энергии, т.е.
плазма называется идеальной. С учетом соотношения (18) неравенство (27) можно переписать как
Другими словами, в идеальной плазме число частиц Nd внутри сферы радиуса d
оказывается много большим единицы. Например, в случае плазмы с температурой Т = 107 К и плотностью n 0 = 1014 см-3 (такие параметры характерны для термоядерной плазмы) дебаевский радиус равен Проведенные выкладки распространяются и на случай неизотермической плазмы, характеризующейся электронной температурой Те и ионной Ti. Действуя точно так же, как и ранее при выводе формул (13) – (23) (изменения касаются только распределений Больцмана (14), в которых теперь стоят свои температуры Те и Ti), получим тот же окончательный результат (23), но с другой длиной экранирования d:
Дебаевский радиус можно рассматривать как масштаб разделения зарядов в плазме. Если пространственные размеры ионизованной среды меньше дебаевского радиуса, то такую среду следует рассматривать скорее не как плазму, а как совокупность свободных зарядов. Если же указанные пространственные размеры велики по сравнению с дебаевским радиусом, ионизованная среда ведет себя как истинная плазма. В этом случае полное число частиц в плазме N удовлетворяет условию Выражение для экранированного потенциала (23) справедливо лишь при выполнении условия (18). С помощью подстановки
Следовательно, формула (23) не применима при Обобщая вышесказанное, приходим в выводу, что несмотря на приближенный характер теории Дебая, она позволяет оценить, при каких параметрах плазму можно описывать законами идеального газа. В заключение этого параграфа приведем несколько полезных формул. Величина kT, называемая термодинамической температурой, в физике плазмы измеряется в практически удобных единицах – электронвольтах (эВ) и обозначается той же буквой Т. При этом
Давление плазмы при условии применимости законов идеального газа, т.е. формулы (27), записывается в виде
Условие применимости формулы (30) выглядит следующим образом:
|

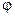 . Согласно распределению Больцмана, концентрация электронов описывается выражением
. Согласно распределению Больцмана, концентрация электронов описывается выражением , (13)
, (13) – заряд электрона,
– заряд электрона,  – радиус-вектор точки поля относительно иона. Для концентрации ионов можно записать выражение, аналогичное (13):
– радиус-вектор точки поля относительно иона. Для концентрации ионов можно записать выражение, аналогичное (13): , (14)
, (14) , когда влиянием потенциала можно пренебречь, условие квазинейтральности плазмы приводит к соотношению n 0 е = n 0 i = n 0.
, когда влиянием потенциала можно пренебречь, условие квазинейтральности плазмы приводит к соотношению n 0 е = n 0 i = n 0. (15)
(15) – гиперболический синус, а слагаемое с δ-функцией отвечает объемной плотности заряда иона в предположении, что этот заряд точечный. Потенциал
– гиперболический синус, а слагаемое с δ-функцией отвечает объемной плотности заряда иона в предположении, что этот заряд точечный. Потенциал 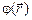 и объемная плотность зарядов
и объемная плотность зарядов  связаны уравнением Пуассона
связаны уравнением Пуассона (16)
(16) (17)
(17) . (18)
. (18) при малых х, получим
при малых х, получим (19)
(19)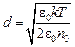 (20)
(20) (21)
(21) . (21*)
. (21*) (22)
(22)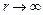 . Окончательно
. Окончательно . (23)
. (23) (24)
(24) , (25)
, (25)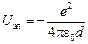 , (26)
, (26) , (27)
, (27) . (28)
. (28)
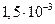 см и Nd =
см и Nd =  .
. . (29)
. (29) , что необходимо для применимости теории Дебая, которая основана на методах статистической физики. Как было установлено ранее, при условии
, что необходимо для применимости теории Дебая, которая основана на методах статистической физики. Как было установлено ранее, при условии  кулоновская энергия плазмы мала по сравнению с тепловой, т.е. изотермическая плазма по своему термодинамическому поведению близка к идеальному газу.
кулоновская энергия плазмы мала по сравнению с тепловой, т.е. изотермическая плазма по своему термодинамическому поведению близка к идеальному газу.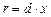 это условие приводится к виду
это условие приводится к виду . (30)
. (30)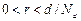 , а потому выражение для кулоновской энергии (26) не является точным, и должно рассматриваться как оценка. Неприменимость выражения (23) при малых r можно увидеть и из следующего факта: интеграл по малой области D, окружающей ион,
, а потому выражение для кулоновской энергии (26) не является точным, и должно рассматриваться как оценка. Неприменимость выражения (23) при малых r можно увидеть и из следующего факта: интеграл по малой области D, окружающей ион,  , который определяет число электронов в указанной области, является расходящимся в силу того, что
, который определяет число электронов в указанной области, является расходящимся в силу того, что  при r << d.
при r << d.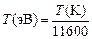 . Суммарная концентрация заряженных частиц в плазме, обозначаемая в дальнейшем n (в рассматриваемом случае n = 2 n 0), измеряется в см-3, а дебаевский радиус – в см, тогда
. Суммарная концентрация заряженных частиц в плазме, обозначаемая в дальнейшем n (в рассматриваемом случае n = 2 n 0), измеряется в см-3, а дебаевский радиус – в см, тогда . (31)
. (31) (мм рт. ст.). (32)
(мм рт. ст.). (32) . (33)
. (33)


