При наличии внешней силы  (например, силы тяжести или силы инерции, если движение рассматривается в неинерциальной системе отчета) уравнение движения частицы вместо (66) следует записывать в виде
(например, силы тяжести или силы инерции, если движение рассматривается в неинерциальной системе отчета) уравнение движения частицы вместо (66) следует записывать в виде
 . (92)
. (92)
Предположим, что сила  постоянна (т.е. не зависит от времени и однородна в пространстве). Тогда с формальной точки зрения действие этой силы аналогично действию стационарного однородного электрического поля. Это означает, что сила
постоянна (т.е. не зависит от времени и однородна в пространстве). Тогда с формальной точки зрения действие этой силы аналогично действию стационарного однородного электрического поля. Это означает, что сила  приводит к дрейфовому движению со скоростью
приводит к дрейфовому движению со скоростью
 . (93)
. (93)
Например, в случае однородного поля силы тяжести  и скорость дрейфа равна
и скорость дрейфа равна
 . (94)
. (94)
Эта скорость дрейфа зависит от отношения  , так что частицы с противоположными зарядами движутся в разные стороны. В плазме вследствие гравитационного дрейфа возникают дрейфовые токи, приводящие к разделению зарядов.
, так что частицы с противоположными зарядами движутся в разные стороны. В плазме вследствие гравитационного дрейфа возникают дрейфовые токи, приводящие к разделению зарядов.
Формулы (93) и (94) получены в нерелятивистском приближении, что справедливо при определенных ограничениях на величину силы 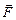 . Поскольку величина дрейфовой скорости
. Поскольку величина дрейфовой скорости
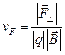
( – перпендикулярная
– перпендикулярная  составляющая силы
составляющая силы 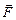 ) в нерелятивистском случае должна быть много меньше скорости света, то необходимо выполнение неравенства
) в нерелятивистском случае должна быть много меньше скорости света, то необходимо выполнение неравенства
 . (95)
. (95)
В частности, в случае однородного электростатического поля неравенство (95) переходит в следующее соотношение:
 . (96)
. (96)
Например, для магнитного поля, индукция которого 1 Тл, формулой (89) можно пользоваться, пока  много меньше 108 В/м.
много меньше 108 В/м.

 (например, силы тяжести или силы инерции, если движение рассматривается в неинерциальной системе отчета) уравнение движения частицы вместо (66) следует записывать в виде
(например, силы тяжести или силы инерции, если движение рассматривается в неинерциальной системе отчета) уравнение движения частицы вместо (66) следует записывать в виде . (92)
. (92) . (93)
. (93) и скорость дрейфа равна
и скорость дрейфа равна . (94)
. (94) , так что частицы с противоположными зарядами движутся в разные стороны. В плазме вследствие гравитационного дрейфа возникают дрейфовые токи, приводящие к разделению зарядов.
, так что частицы с противоположными зарядами движутся в разные стороны. В плазме вследствие гравитационного дрейфа возникают дрейфовые токи, приводящие к разделению зарядов.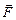 . Поскольку величина дрейфовой скорости
. Поскольку величина дрейфовой скорости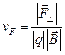
 – перпендикулярная
– перпендикулярная  составляющая силы
составляющая силы  . (95)
. (95) . (96)
. (96) много меньше 108 В/м.
много меньше 108 В/м.


