Важное следствие адиабатической инвариантности величин 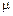 и Фм заключается в следующем. Поскольку сохраняются как магнитный момент частицы, так и ее кинетическая энергия, то по мере вхождения частицы в область схождения магнитных силовых линий ее поперечная кинетическая энергия
и Фм заключается в следующем. Поскольку сохраняются как магнитный момент частицы, так и ее кинетическая энергия, то по мере вхождения частицы в область схождения магнитных силовых линий ее поперечная кинетическая энергия  будет возрастать, а продольная
будет возрастать, а продольная  – уменьшаться. Если возрастание индукции магнитного поля достаточно велико, то в результате торможения составляющая скорости
– уменьшаться. Если возрастание индукции магнитного поля достаточно велико, то в результате торможения составляющая скорости  обратится в нуль, а затем поменяет знак. После этого величина
обратится в нуль, а затем поменяет знак. После этого величина  будет увеличиваться в направлении уменьшения магнитной индукции, а ее поперечная скорость будет уменьшаться. Таким образом, частицы отражаются от области сходящихся магнитных силовых линий. Это явление называется магнитным отражением, а область растущего магнитного поля – магнитным зеркалом или магнитной пробкой. Комбинация двух коаксиальных зеркал, расположенных напротив друг друга, называется магнитной бутылкой (рис. 5). Такую конфигурацию можно использовать для удержания плазмы: заряженные частицы будут попеременно отражаться то одним, то другим зеркалом и, следовательно, окажутся захваченными магнитной бутылкой. К сожалению, магнитные бутылки не являются идеальными устройствами для удержания плазмы.
будет увеличиваться в направлении уменьшения магнитной индукции, а ее поперечная скорость будет уменьшаться. Таким образом, частицы отражаются от области сходящихся магнитных силовых линий. Это явление называется магнитным отражением, а область растущего магнитного поля – магнитным зеркалом или магнитной пробкой. Комбинация двух коаксиальных зеркал, расположенных напротив друг друга, называется магнитной бутылкой (рис. 5). Такую конфигурацию можно использовать для удержания плазмы: заряженные частицы будут попеременно отражаться то одним, то другим зеркалом и, следовательно, окажутся захваченными магнитной бутылкой. К сожалению, магнитные бутылки не являются идеальными устройствами для удержания плазмы.
Сформулируем условие удержания частицы. Пусть в начальной момент времени скорость частицы  составляет с направлением вектора магнитной индукции
составляет с направлением вектора магнитной индукции  угол
угол  . В некоторый другой момент времени скорость частицы, не изменившись по величине, будет образовывать угол
. В некоторый другой момент времени скорость частицы, не изменившись по величине, будет образовывать угол  с изменившимся вектором
с изменившимся вектором  .
.

Рис. 5. Магнитная бутылка
Из условия сохранения магнитного момента частицы вытекает, что
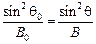 . (123)
. (123)
Отражение частицы произойдет в точке, где  , т.е. магнитное поле имеет величину
, т.е. магнитное поле имеет величину
 . (124)
. (124)
Если максимальное значение магнитного поля равно  , то все частицы, для которых
, то все частицы, для которых
 , (125)
, (125)
будут отражаться. Помимо величины  магнитная бутылка характеризуется величиной
магнитная бутылка характеризуется величиной  магнитного поля в ее центре и зеркальным отношением
магнитного поля в ее центре и зеркальным отношением  . Из формулы (125) видно, что все частицы, для скоростей которых начальный угол удовлетворяет соотношению
. Из формулы (125) видно, что все частицы, для скоростей которых начальный угол удовлетворяет соотношению  , будут уходить из бутылки через края системы зеркал. В результате возникает конус потерь – конус скоростей с углом раствора, равным
, будут уходить из бутылки через края системы зеркал. В результате возникает конус потерь – конус скоростей с углом раствора, равным  .
.
Для удержания плазмы рядом преимуществ обладает системы, у которых нет границ. Примером такой системы является тороидальный магнитный соленоид (рис. 6). Однако в этом случае возникает радиальная неоднородность поля и связанный с ней градиентный дрейф плазмы. Более совершенными являются конфигурации, в которых на тороидальное магнитное поле накладывается магнитное поле токов самой плазмы (как в токамаках) либо магнитное поле внешних винтовых проводников (как в стеллараторах) и т.д.

Рис. 6. Тороидальный магнитный соленоид
Однако и здесь проявляется основная проблема большинства схем удержания плазмы – возникновение неустойчивостей, приводящих к быстрой потере частиц из магнитной ловушки.
Примером природной магнитной ловушки является магнитосфера Земли. Заряженные частицы солнечного и космического происхождения, захваченные магнитным полем Земли, образуют так называемые радиационные пояса Ван-Аллена. Области вблизи магнитных полюсов, где магнитное поле увеличивается, являются магнитными зеркалами. Заряженные частицы двигаются по спиралям вдоль линий индукции в меридиональном направлении и отражаются вблизи одного из магнитных полюсов, меняя направление движения на обратное (рис. 7). Благодаря этому заряженные частицы длительное время удерживаются вблизи Земли, в результате чего и образуются радиационные пояса.

Рис. 7. Радиационные пояса Земли

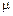 и Фм заключается в следующем. Поскольку сохраняются как магнитный момент частицы, так и ее кинетическая энергия, то по мере вхождения частицы в область схождения магнитных силовых линий ее поперечная кинетическая энергия
и Фм заключается в следующем. Поскольку сохраняются как магнитный момент частицы, так и ее кинетическая энергия, то по мере вхождения частицы в область схождения магнитных силовых линий ее поперечная кинетическая энергия  будет возрастать, а продольная
будет возрастать, а продольная  – уменьшаться. Если возрастание индукции магнитного поля достаточно велико, то в результате торможения составляющая скорости
– уменьшаться. Если возрастание индукции магнитного поля достаточно велико, то в результате торможения составляющая скорости  обратится в нуль, а затем поменяет знак. После этого величина
обратится в нуль, а затем поменяет знак. После этого величина  составляет с направлением вектора магнитной индукции
составляет с направлением вектора магнитной индукции  угол
угол  . В некоторый другой момент времени скорость частицы, не изменившись по величине, будет образовывать угол
. В некоторый другой момент времени скорость частицы, не изменившись по величине, будет образовывать угол  с изменившимся вектором
с изменившимся вектором  .
.
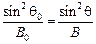 . (123)
. (123) , т.е. магнитное поле имеет величину
, т.е. магнитное поле имеет величину . (124)
. (124) , то все частицы, для которых
, то все частицы, для которых , (125)
, (125) магнитного поля в ее центре и зеркальным отношением
магнитного поля в ее центре и зеркальным отношением  . Из формулы (125) видно, что все частицы, для скоростей которых начальный угол удовлетворяет соотношению
. Из формулы (125) видно, что все частицы, для скоростей которых начальный угол удовлетворяет соотношению  , будут уходить из бутылки через края системы зеркал. В результате возникает конус потерь – конус скоростей с углом раствора, равным
, будут уходить из бутылки через края системы зеркал. В результате возникает конус потерь – конус скоростей с углом раствора, равным  .
.




