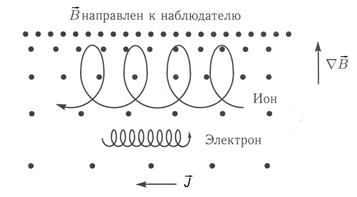
Градиентный дрейф
Инвариантность магнитного момента заряженной частицы в слабо неоднородном пространстве в магнитном поле позволяет объяснить явление градиентного дрейфа, скорость которого направлена перпендикулярно силовым линиям магнитного поля. Если рассматривать частицу, движущуюся по ларморовской окружности, как элементарный «магнитик» с магнитным моментом
Вследствие слабой неоднородности магнитного поля силу
Из формулы (127) вытекают следующие следствия: а) скорость градиентного дрейфа перпендикулярна как силовым линиям магнитного поля, так и градиенту поля; б) направление градиентного дрейфа зависит от знака заряда, так что электроны и положительно заряженные ионы плазмы дрейфуют в противоположные стороны, т.е. возникает дрейфовый ток (рис. 8).
Рис. 8. Градиентный дрейф Еще раз подчеркнем, что рассматриваемый дрейф представляет собой смещение ведущих центров, впрочем, мало отличающихся от смещений самих частиц, за счет сил, перпендикулярных магнитным силовым линиям.
ЛИТЕРАТУРА
1. Физическая энциклопедия / Под ред. А.М. Прохорова. Статьи: Плазма. Управляемый термоядерный синтез. Дрейф заряженных частиц. – М.: Советская энциклопедия, 1990. 2. Арцимович Л.А. Элементарная физика плазмы. – М.: Атомиздат, 1966. 3. Франк-Каменецкий Д.А. Лекции по физике плазмы. – М.: Атомиздат, 1968. 4. Арцимович Л.А. Управляемые термоядерные реакции. – М.: Физматгиз, 1961. 5. Голант В.Е., Жилинский А.П., Сахаров И.Е. Основы физики плазмы. – М.: Атомиздат, 1977. 6. Роуз Д., Кларк М. Физика плазмы и управляемые термоядерные реакции. – М.: Госатомиздат, 1963. 7. Биттенкорт Ж.А. Основы физики плазмы. – М.: Физматлит, 2009. 8. Синельников К.Д., Руткевич Б.Н. Лекции по физике плазмы. – Харьков: Изд-во Харьковского университета, 1964. 9. Трубников Б.А. Введение в теорию плазмы. – М.: Московский инженерно-физический институт, 1969. 10. Матвеев А.Н. Механика и теория относительности. – М.: Высшая школа, 1976. 11. Иродов И.Е. Задачи по общей физике. – М.: Наука, 1988. 12. Франк-Каменецкий Д.А. Плазма – четвертое состояние вещества. – М.: Госатомиздат, 1968.
СОДЕРЖАНИЕ
1. Основные понятия физики плазмы………………………….…3 2. Плазменная (лэнгмюровская) частота……………………..…...6 3. Экранирование зарядов в плазме. Дебаевский радиус………..9 4. Элементарные процессы в плазме…………………………….13 5. Термоядерная плазма. Критерий Лоусона…………………....18 6. Лазерный термоядерный синтез (ЛТС)……………………….24 7. Движение заряженных частиц в электромагнитных полях………………………………………26 8. Однородное электрическое поле……………………………...27 9. Однородное стационарное магнитное поле…………………..28 10. Однородные электростатические и магнитостатические поля…………………………………….31 11. Дрейф под воздействием внешней силы…………………….33 12. Магнитный момент частицы в магнитном поле……………34 13. Адиабатическая инвариантность магнитного момента…….35 14. Магнитные зеркала…………………………………………...41 15. Градиентный дрейф…………………………………………..44 Литература………………….……………………………..............46
|

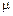 , то в условиях применимости дрейфового приближения (радиус ларморовской окружности много меньше характерной длины l поля, на которой происходит существенное изменение магнитного поля) частицу можно характеризовать магнитной энергией
, то в условиях применимости дрейфового приближения (радиус ларморовской окружности много меньше характерной длины l поля, на которой происходит существенное изменение магнитного поля) частицу можно характеризовать магнитной энергией  . В рассматриваемой ситуации вектор
. В рассматриваемой ситуации вектор  всегда направлен против вектора
всегда направлен против вектора  (диамагнетизм плазмы), так что
(диамагнетизм плазмы), так что  . Последняя формула показывает, что W м убывает с уменьшением индукции магнитного поля, а потому центр ларморовского кружка будет стремиться покинуть область сильного поля. Ответственной за это будет сила
. Последняя формула показывает, что W м убывает с уменьшением индукции магнитного поля, а потому центр ларморовского кружка будет стремиться покинуть область сильного поля. Ответственной за это будет сила  , определяемая известным соотношением
, определяемая известным соотношением . (126)
. (126)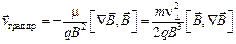 . (127)
. (127)