Магнитный момент частицы в магнитном поле
В этом параграфе рассматривается движение частицы в слабо изменяющемся магнитном поле. Это означает, что индукция магнитного поля мало меняется на расстояниях порядка циклотронного радиуса частицы либо незначительно меняется за время одного оборота частицы по циклотронной окружности. В упомянутых случаях магнитный момент частицы, определяемый по аналогии с магнитным моментом кругового тока, сохраняет, хотя и приближенно, свое значение. Как будет показано дальше, этот факт во многих практически интересных случаях позволяет значительно упростить анализ движения плазменных частиц. Напомним, что магнитный момент
Частица с зарядом q, движущаяся по окружности радиуса R с периодом T, создает замкнутый ток силы
При движении в магнитном поле с индукцией В, как было установлено ранее,
так что магнитный момент частицы оказывается равным
где
Адиабатическая инвариантность магнитного момента
В рассматриваемом контексте термин «адиабатический» означает «медленно изменяющийся», так что под адиабатическим инвариантом понимается величина, остающаяся постоянной при движении системы с медленно меняющимися параметрами. Допустим, что однородное в пространстве магнитное поле изменяется с течением времени, причем достаточно медленно. Это означает, что время
Выберем в качестве контура Г окружность радиуса
Рис. 4. Направление вихревого электрического поля для случая медленно возрастающего магнитного поля (
Вследствие малости величины
где
Величина d Ф отрицательна, если q >0 (контур проходится по часовой стрелке), в то время как для q <0 выполняется условие d Ф>0 (контур проходится против часовой стрелки). В итоге, если
Вследствие выполнения условия
Поскольку
Из соотношений (105), (106) вытекает, что В приведенном выводе использовалось условие малости изменения циклотронного радиуса за один период, которое эквивалентно условию малости относительно изменения магнитного поля за период циклотронного обращения:
Перейдем теперь к изучению движения частицы в неизменяющемся во времени, но слабо изменяющемся в пространстве магнитном поле. Если поле возрастает, то магнитные силовые линии образуют слабо сходящийся пучок. Совместим начало системы координат с мгновенным положением ведущего центра, а ось OZ направим вдоль вектора магнитной индукции. Как выясняется. вследствие неоднородности магнитного поля наряду с продольной составляющей Bz неизбежно будет существовать радиальная составляющая Для вычисления этой силы воспользуемся уравнением Максвелла
На следующем этапе мы будем интересоваться только сглаженным движением ведущего центра, что достигается усреднением силы Лоренца за период вращения (или за множество таких периодов). Получаемое в результате уравнение движения ведущего центра носит название приближения Альфвена, или приближения ведущего центра, или дрейфового приближения. Дрейфовое приближение применимо, если магнитное поле является достаточно сильным. Тогда движение частицы можно представить как суперпозицию трех видов движений: 1) быстрое движение по циклотронной окружности вокруг ведущего центра; 2) движение ведущего центра вдоль силовой линии магнитного поля; 3) медленное дрейфовое движение ведущего центра поперек магнитного поля. При этом необходимо, чтобы характерная длина, на которой магнитное поле заметно изменяется, была много больше радиуса циклотронной орбиты частицы. Процедура усреднения за период для некоторой величины A (
причем здесь учтено, что вследствие медленности изменения магнитного поля величину Т и циклотронную частоту
Второе слагаемое в (110) дает нулевой вклад:
Далее, имеет место соотношение
при выводе которого было принято, что магнитное поле слабо изменяется в пределах орбиты частицы, а потому медленно изменяющуюся функцию
Из (110) – (112) вытекает уравнение для величины
в котором величину
Из (113) и (115) вытекает, что в пределах орбиты частицы, т.е. при
что и ожидалось. Как и в случае постоянного магнитного поля, разложим скорость частицы на составляющие
Величина
Умножая соотношение (112) на
Здесь уместно напомнить, что
вытекает, что
Последний результат совпадает с соотношением (105), так что (120) снова подтверждает постоянство магнитного момента. Итак, магнитный момент частицы остается постоянным при движении частицы в медленно изменяющемся либо в пространстве, либо во времени магнитном поле, что и означает адиабатическую инвариантность магнитного момента. Рассчитаем магнитный поток через поверхность, опирающуюся на циклотронную орбиту частицы:
Следовательно,
так что из инвариантности магнитного момента частицы вытекает инвариантность магнитного потока и наоборот. Инвариантность величины Фм означает, что частица движется по поверхности магнитной трубки, т.е. по поверхности, образованной линиями магнитной индукции.
|

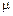 кругового тока силы I, обтекающий участок плоской поверхности, площадь которого равна S, определяется соотношением
кругового тока силы I, обтекающий участок плоской поверхности, площадь которого равна S, определяется соотношением . (97)
. (97) . Следовательно, такому движению частицы можно сопоставить магнитный момент
. Следовательно, такому движению частицы можно сопоставить магнитный момент . (98)
. (98) ;
;  , (99)
, (99) , (100)
, (100) – кинетическая энергия частицы, отвечающая составляющей скорости в плоскости, перпендикулярной линиям индукции магнитного поля, часто называемая поперечной кинетической энергией.
– кинетическая энергия частицы, отвечающая составляющей скорости в плоскости, перпендикулярной линиям индукции магнитного поля, часто называемая поперечной кинетической энергией. , за которое индукция магнитного поля заметно изменяет свое значение, удовлетворяет условию адиабатичности
, за которое индукция магнитного поля заметно изменяет свое значение, удовлетворяет условию адиабатичности  . Согласно закону электромагнитной индукции, изменяющееся магнитное поле порождает вихревое электрическое поле
. Согласно закону электромагнитной индукции, изменяющееся магнитное поле порождает вихревое электрическое поле  . При этом циркуляция вектора
. При этом циркуляция вектора  . (101)
. (101) , тогда вихревое электрическое поле будет направлено вдоль этой окружности (рис. 4).
, тогда вихревое электрическое поле будет направлено вдоль этой окружности (рис. 4).
 )
) циклотронный радиус мало изменяется за один период. Поскольку электрическое поле действует на частицу с силой
циклотронный радиус мало изменяется за один период. Поскольку электрическое поле действует на частицу с силой  , то изменение поперечной кинетической энергии за один период равно
, то изменение поперечной кинетической энергии за один период равно , (102)
, (102) – элемент перемещения вдоль траектории, которая при выполнении условия адиабатичности мало отличается от окружности радиуса R. По этой причине интеграл в формуле (102) можно вычислить как интеграл по замкнутому контуру в виде циклотронной окружности фиксированного радиуса:
– элемент перемещения вдоль траектории, которая при выполнении условия адиабатичности мало отличается от окружности радиуса R. По этой причине интеграл в формуле (102) можно вычислить как интеграл по замкнутому контуру в виде циклотронной окружности фиксированного радиуса: . (103)
. (103) положительна независимо от знака заряда:
положительна независимо от знака заряда: . (104)
. (104) можно заменить производной
можно заменить производной  , так что
, так что . (105)
. (105) , то
, то . (106)
. (106) , т.е. магнитный момент частицы сохраняется.
, т.е. магнитный момент частицы сохраняется. . (107)
. (107) (в цилиндрической системе координат), благодаря которой частица, описывающая окружность около ведущего центра, будет испытывать силу, пропорциональную
(в цилиндрической системе координат), благодаря которой частица, описывающая окружность около ведущего центра, будет испытывать силу, пропорциональную  , которое в указанной выше цилиндрической системе координат выглядит
, которое в указанной выше цилиндрической системе координат выглядит  следующим образом:
следующим образом: . (108)
. (108) , z), аргументы которой берутся в точках траектории частицы, а потому являются функциями времени, определяется как
, z), аргументы которой берутся в точках траектории частицы, а потому являются функциями времени, определяется как , (109)
, (109) можно считать постоянными. Из соотношения (108) вытекает, что
можно считать постоянными. Из соотношения (108) вытекает, что . (110)
. (110) . (111)
. (111) , (112)
, (112) можно было вынести за знак интеграла. Последнее равенство в (112) обосновывается тем, что в интересующей нас области пространства компоненты
можно было вынести за знак интеграла. Последнее равенство в (112) обосновывается тем, что в интересующей нас области пространства компоненты  магнитного поля и их производные очень малы. Условием применимости соотношения (112) является неравенство
магнитного поля и их производные очень малы. Условием применимости соотношения (112) является неравенство . (113)
. (113)
 , (114)
, (114) можно считать практически не зависящей от
можно считать практически не зависящей от  . (115)
. (115) , выполняется неравенство
, выполняется неравенство , (116)
, (116) и
и  . Поскольку в рассматриваемой ситуации линии магнитной индукции сгущаются (или, наоборот, расходятся) не очень сильно, то их наклон к оси OZ достаточно мал. По этой причине проекция
. Поскольку в рассматриваемой ситуации линии магнитной индукции сгущаются (или, наоборот, расходятся) не очень сильно, то их наклон к оси OZ достаточно мал. По этой причине проекция  . В итоге уравнение движения для продольной компоненты скорости (с учетом процедуры усреднения по периоду движения) записывается в виде
. В итоге уравнение движения для продольной компоненты скорости (с учетом процедуры усреднения по периоду движения) записывается в виде . (117)
. (117) . Подставляя соотношение (115) в (117), получим
. Подставляя соотношение (115) в (117), получим . (118)
. (118) и учитывая, что
и учитывая, что  , получим
, получим . (119)
. (119) , т.е. для стационарного поля, когда
, т.е. для стационарного поля, когда  ,
,  . Из условия сохранения кинетической энергии в стационарном магнитном поле
. Из условия сохранения кинетической энергии в стационарном магнитном поле ,
, . (120)
. (120) . (121)
. (121) , (122)
, (122)


