Движение заряженных частиц в электромагнитных полях
Динамическое поведение плазмы определяется как внутренними полями, создаваемыми частицами плазмы, так и внешними полями. Изучение этого поведения важно для анализа динамических процессов, протекающих в плазме, и понимания принципов действия различных плазменных устройств, например, систем магнитного удержания плазмы. При этом выясняется, что движение частиц в плазме полностью описывается законами классической механики, поскольку обычно импульс частиц плазмы достаточно велик, плотность плазмы не очень большая, а соответствующие длины волн де Бройля намного меньше расстояния между частицами. Плазма проявляет квантовые свойства только при очень больших плотностях и очень низких температурах. Более того, как правило, релятивистские эффекты малы, и для описания движения частиц достаточно ограничиться нерелятивистским приближением. Итак, в пренебрежении столкновениями с другими частицами и излучением уравнение движения частицы с зарядом q и массой m можно записать в виде
где
(
Если электромагнитное поле не зависит от времени то, как известно из курса общей физики, остается неизменной сумма кинетической и электрической потенциальной энергий частиц
(
где
8. Однородное электрическое поле (
В случае постоянного стационарного электрического поля уравнение движения частицы
легко интегрируется:
где
где
9. Однородное стационарное магнитное поле
В данном случае уравнение движения выглядит следующем образом:
Разложим скорость
Поскольку вектор
в направлении, параллельном магнитному полю, и
в направлении, перпендикулярном магнитному полю. Уравнение (71) показывает, что компонента скорости частицы вдоль вектора Как уже отмечалось, магнитное поле не изменяет кинетической энергии частицы. Из этого факта и только что полученного условия Приведем решение уравнения (72) в декартовой системе координат, в которой вектор
и учитывая, что
(знак + перед циклотронной частотой соответствует положительно заряженной частице, знак – – отрицательно заряженной), перепишем уравнение (72) в виде двух уравнений:
Из (75) вытекает, что вторые производные компонент vx и vy удовлетворяют уравнению колебаний линейно гармонического осциллятора с частотой
следовательно,
где постоянная интегрирования
Из соотношений (77) получаем условие постоянства величины Из условия
В (79) были использованы обозначения:
Величина
Вектор Из соотношений (79) и (80) видно, что траекторией частицы в плоскости, нормальной вектору магнитной индукции, является окружность радиуса
Центр этой окружности, являющейся мгновенным центром вращения частицы, называется ведущим центром. Полная траектория частицы получается из суперпозиции движения по окружности (с постоянной скоростью Приведем две полезные формулы для вычисления циклотронной частоты: для электрона Отметим, что в релятивистском случае
|

 , (64)
, (64) – импульс частицы,
– импульс частицы,  – ее скорость.
– ее скорость. , (65)
, (65) – релятивистский фактор) или в нерелятивистском приближении
– релятивистский фактор) или в нерелятивистском приближении . (66)
. (66) :
: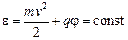 , (67)
, (67) – потенциал электростатического поля, так что
– потенциал электростатического поля, так что 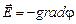 ). Этот факт непосредственно следует из того, что при любой конфигурации магнитостатического поля оно не совершает механической работы над частицей. Соотношение (67) записано в нерелятивистском приближении, которое в общем случае следует записывать в виде
). Этот факт непосредственно следует из того, что при любой конфигурации магнитостатического поля оно не совершает механической работы над частицей. Соотношение (67) записано в нерелятивистском приближении, которое в общем случае следует записывать в виде ,
, – кинетическая энергия релятивистской частицы. В дальнейшем, если не оговорено противное, будет использоваться нерелятивистская механика. Особое внимание будет уделено однородным в пространстве и постоянным во времени полям, поскольку многие более сложные случаи могут рассматриваться как возмущения по отношению к этой простой ситуации.
– кинетическая энергия релятивистской частицы. В дальнейшем, если не оговорено противное, будет использоваться нерелятивистская механика. Особое внимание будет уделено однородным в пространстве и постоянным во времени полям, поскольку многие более сложные случаи могут рассматриваться как возмущения по отношению к этой простой ситуации. )
) ,
, ,
, – начальный импульс частицы. Повторное интегрирование дает выражение для положения частицы как функции времени
– начальный импульс частицы. Повторное интегрирование дает выражение для положения частицы как функции времени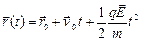 , (68)
, (68) – положение частицы, а
– положение частицы, а  – скорость частицы в начальный момент времени. Частица движется с постоянным ускорением
– скорость частицы в начальный момент времени. Частица движется с постоянным ускорением  в направлении
в направлении  , если q >0, и в противоположном направлении, если q <0. В направлении, перпендикулярном электрическому полю, ускорение отсутствует, и соответствующая компонента скорости остается постоянной.
, если q >0, и в противоположном направлении, если q <0. В направлении, перпендикулярном электрическому полю, ускорение отсутствует, и соответствующая компонента скорости остается постоянной.
 . (69)
. (69) и перпендикулярную ему
и перпендикулярную ему 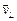 , тогда
, тогда . (70)
. (70) перпендикулярен
перпендикулярен  , то из уравнения (70) вытекают два следующих уравнения:
, то из уравнения (70) вытекают два следующих уравнения: =0, (71)
=0, (71) , (72)
, (72) = const. Поскольку в силу (72) ускорение частицы всегда перпендикулярно вектору
= const. Поскольку в силу (72) ускорение частицы всегда перпендикулярно вектору  , причем из уравнения (72) вытекает, что
, причем из уравнения (72) вытекает, что  . Величина
. Величина  (
(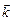 – орт, задающий положительное направление этой оси). Тогда, представляя вектор
– орт, задающий положительное направление этой оси). Тогда, представляя вектор 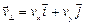 , (73)
, (73) , (74)
, (74) ;
;  . (75)
. (75) , (76)
, (76) ,
,  , (77)
, (77) зависит от отношения начальных скоростей vx (0) и vy (0):
зависит от отношения начальных скоростей vx (0) и vy (0):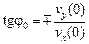 . (78)
. (78) , равной модулю перпендикулярной составляющей скорости, как это и должно быть.
, равной модулю перпендикулярной составляющей скорости, как это и должно быть. и соотношений (77) легко получить зависимость координат частицы от времени:
и соотношений (77) легко получить зависимость координат частицы от времени: ,
,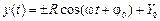 , (79)
, (79) .
. ;
;  . (80)
. (80) носит название циклотронного или ларморовского радиуса
носит название циклотронного или ларморовского радиуса . (81)
. (81) задает начальное положение частицы.
задает начальное положение частицы. :
: . (82)
. (82) , для протона
, для протона  . В обоих случаях В выражено в теслах.
. В обоих случаях В выражено в теслах. , а циклотронный радиус равен
, а циклотронный радиус равен 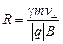 .
.


