A (В С))↔((А В) (А С)).
7. Закони Моргана: 1) Перший закон Моргана: ~ (A 2) Другий закон Моргана: ~ (A 1. Закон подвійного заперечення – це логічний закон, згідно з яким заперечення дає твердження, з твердження випливає його подвійне заперечення, а подвійне заперечення є рівносильним твердженню. З цього закону випливають: 1) Закон зняття подвійного заперечення, згідно з яким повторене двічі заперечення дає твердження: Схема: ~ ~ A→A (Коли неправильно, що неправильно, що А, то А). Якщо неправильно, що він не є студентом то він є студентом. 2) Закон введення подвійного заперечення, згідно з яким з твердження випливає його подвійне заперечення: Схема: А→~ ~А (Якщо А, то неправильно, що не-А). Якщо студент склав іспит з філософії, то неправильно, що він не склав цей іспит. 3) Повний закон подвійного заперечення, згідно з яким подвійне заперечення рівносильне відповідному твердженню: Схема: ~ ~А↔А (Неправильно, що не-А, тоді і тільки тоді, коли А). Неправильно, що ця книга є нецікавою тоді і тільки тоді, коли вона є цікавою. 2. Закон ідемпотентності – це логічний закон, який стверджує, що повторення положення через «і» («кон'юнкція») чи «або» («диз'юнкція») рівнозначно самому висловлюванню. З цього закону випливають: 1) Закон ідемпотентності для кон'юнкції, який стверджує, що повторення будь-якого положення через «і» («кон'юнкція») рівнозначне самому висловлюванню: Схема: (A «Літак має блакитний колір» і «Літак має блакитний колір» те ж, що «Літак має блакитний колір». 2) Закон ідемпотентності для диз'юнкції, який стверджує, що повторення будь-якого положення через «або» («диз'юнкція») рівнозначне самому висловлюванню: Схема: (A «Літак має блакитний колір» або «Літак має блакитний колір» те ж, що «Літак має блакитний колір». 3. Закон комутативності – це логічний закон, який дозволяє міняти місцями висловлювання, які пов'язані логічними зв'язками «і» («кон'юнкція») і «або» («диз'юнкція»). З цього закону випливають: 1) Закон комутативності для кон'юнкції, який дозволяє міняти місцями висловлювання, які пов'язані логічною зв'язкою «і» («кон'юнкція»): Схема: (A «Дитина має цукерку і іграшку» те ж, що «Дитина має іграшку і цукерку». 2) Закон комутативності для диз'юнкції, який дозволяє міняти місцями висловлювання, які пов'язані логічною зв'язкою «або» («диз'юнкція»): Схема: (A «Дитина має цукерку або іграшку» те ж, що «Дитина має іграшку або цукерку». 4. Закон контрапозиції – це логічний закон, який дозволяє за допомогою заперечення міняти місцями «антецедент» (перше висловлювання – засновок) і «консеквент» (друге висловлювання – наслідок) імплікації, яка поєднує прості судження логічною зв'язкою «якщо, то»: З цього закону випливають: Закони простої контрапозиції: 1) Перший закон простої контрапозиції, згідно з яким, якщо з першого висловлювання випливає друге висловлювання, то із заперечення другого висловлювання випливає заперечення першого висловлювання: Схема: (A→В)→(~В → ~A) (Коли відомо, що якщо А, то В, то якщо не-В, то не-А). Якщо правильно, що він вчиться у вищій школі, то він студент, то правильно, що якщо він не є студентом, то він не вчиться у вищій школі. 2) Другий закон простої контрапозиції, згідно з яким, якщо із заперечення першого висловлювання випливає заперечення другого висловлювання, то з другого висловлювання випливає перше висловлювання: Схема: (~A→~В)→(В→A) (Коли відомо, що якщо не-А, то не-В, то якщо В, то А). Якщо правильно, що він не є студентом, то він не вчиться у вищій школі, то правильно, що якщо він вчиться у вищій школі, то він студент. 3) Третій закон простої контрапозиції, згідно з яким, якщо з першого висловлювання випливає заперечення другого висловлювання, то з другого висловлювання випливає заперечення першого висловлювання: Схема: (A→~В)→(В→~A) (Коли відомо, що якщо А, то не-В, то якщо В, то не-А). Якщо правильно, що якщо він є студентом, то він не є школярем, тоді правильно, що якщо він є школярем, то він не є студентом. 4) Четвертий закон простої контрапозиції, згідно з яким, якщо із заперечення першого висловлювання випливає друге висловлювання, то із заперечення другого висловлювання випливає перше висловлювання: Схема: (~A→В)→(~В→A) (Коли відомо, що якщо не-А, то В, то якщо не-В, то А). Якщо правильно, що якщо студент не був в університеті, то він був за межами його, тоді правильно, що якщо він не був за його межами, то він був в університеті. Закони складної контрапозиції: 1) Перший закон складної контрапозиції, згідно з яким з першого і другого висловлювань випливає третє висловлювання тоді і тільки тоді, коли з першого висловлювання і заперечення третього висловлювання випливає заперечення другого висловлювання: Схема: ((A і тільки тоді з А і не-С випливає не-В). Якщо він вступив до університету і отримав диплом, то він став фахівцем, тоді і тільки тоді, якщо він вступив до університету і не став фахівцем, то він ще не отримав диплом. 2) Другий закон складної контрапозиції, згідно з яким з першого висловлювання випливає друге або третє висловлювання тоді і тільки тоді, коли із заперечення другого висловлювання випливає заперечення першого висловлювання або третє висловлювання: Схема: (A→;(В Якщо він зробив телефонний дзвінок, то він зробив його із стаціонарного або мобільного телефону тоді і тільки тоді, коли, якщо він не зробив телефонний дзвінок із стаціонарного телефону, то він не зробив телефонний дзвінок або зробив його з мобільного телефону. 5. Закон асоціативності – це логічний закон, який дозволяє по-різному групувати висловлювання, поєднані за допомогою логічних зв'язок «і» («кон'юнкція») і «або» («диз'юнкція») і т.п. З цього закону випливають: 1) Закон асоціативності для кон'юнкції, який дозволяє по-різному об'єднувати висловлювання, поєднані за допомогою логічної зв'язки «і» («кон'юнкція»): Схема: ((A Олена і Алла є подругами Марині тоді і тільки тоді, коли Олена є подругою Аллі і Марині. 2) Закон асоціативності диз'юнкції, який дозволяє по-різному об'єднувати висловлювання, поєднані за допомогою логічної зв'язки «або» («диз'юнкція»): Схема: ((A (В або С)). Олена або Алла або Марина є подругами тоді і тільки тоді, коли Олена або Алла або Марина є подругами. 6. Закон дистрибутивності – це логічний закон, який дозволяє розподіляти одну логічну зв'язку відносно іншої. З цього закону випливають: 1) Закон дистрибутивності кон'юнкції відносно диз'юнкції, за яким у формулах можна розподіляти кон'юнкцію відносно диз'юнкції: Схема: (A (А і В)або (А і С). Театр відвідали Олена разом з Аллою або Ларисою тоді і тільки тоді, коли театр відвідали Олена разом з Аллою або Олена разом з Ларисою. 2) Закон дистрибутивності диз'юнкції відносно кон'юнкції, за яким у формулах можна розподіляти диз'юнкцію відносно кон'юнкції: Схема: (A (А або В) і(А або С). Театр відвідали Олена або Алла разом з Ларисою тоді і тільки тоді, коли театр відвідали Олена або Алла і Олена або Лариса. 7. Закони Моргана – це логічні закони, які пов'язують заперечення, кон'юнкцію і диз'юнкцію: З цього закону випливають: 1) Перший закон Моргана, за яким заперечення кон'юнкції еквівалентне диз'юнкції заперечень: Схема: ~ (A Неправильно, що Олена написала розповідь і поему тільки у тому разі, якщо Олена не написала розповідь або не написала поему. 2) Другий закон Моргана, за яким заперечення диз'юнкції еквівалентне кон'юнкції заперечень: Схема: ~ (A Неправильно, що Олена написала розповідь або поему тоді і тільки тоді, якщо Олена не написала ні розповіді, ні поеми. Такими є основні закони правильного мислення. Їх дотримання є необхідною умовою точності, ясності, послідовності і аргументованості самого мислення.
|

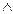 В)↔(~А
В)↔(~А  ~В);
~В);


