Для экономических специальностей заочной формы обучения. 1. Студент знает 20 из 25 вопросов программы
Вариант 3 1. Студент знает 20 из 25 вопросов программы. Зачет считается сданным, если студент ответит не менее, чем на два из трех имеющихся в билете вопросов. Какова вероятность того, что студент сдаст зачет? 2. Для проверки собранной схемы последовательно послано три одиночных импульса. Вероятности прохождения каждого из них не зависят от того, прошли остальные или нет, и соответственно равны 0,5, 0,4 и 0,3. Определить вероятность того, что пройдет хотя бы один из посланных импульсов. 3. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров. 4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа. а) Вероятность попадания в цель при одном выстреле из орудия р =0,85. Найти вероятность того, что в цель попадет не менее двух снарядов, если будет сделано 3 выстрела. б) В установленном технологическом процессе фабрика выпускает в среднем 75% продукции 1-го типа. Найти вероятность того, что в партии из 500 изделий окажется изделий 1-го типа: а) ровно 390, б) больше 370, но меньше 400. 5. Дан перечень возможных значений дискретной случайной величины Х: x 1=2, x 2=4, x 3=6, а также даны математическое ожидание этой величины M[ X ]=4,2 и ее квадрата M[ X 2]=19,6. Найти закон распределения случайной величины Х. 6. Непрерывная случайная величина Х задана функцией распределения
Найти: а) параметр k; б) математическое ожидание; в) дисперсию. 7. Известны математическое ожидание а =6 и среднее квадратичное отклонение s=4 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (1, 8); б) отклонения этой величины от математического ожидания не более, чем на d=3. 8. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса, используя упрощенный метод вычислений, и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
9. Методом наименьших квадратов подобрать функцию
ВЫСШАЯ МАТЕМАТИКА Контрольная работа №3
|


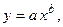 по табличным данным и сделать чертеж.
по табличным данным и сделать чертеж.


