Теперь рассмотрим аналогичную задачу для замкнутой системы.

Что изменилось с появлением замкнутого контура? Во-первых, уже не требуется, чтобы передаточные функции регулятора  и объекта
и объекта  были устойчивыми. Во-вторых, требуется обеспечить устойчивость замкнутой системы. В-третьих, поскольку
были устойчивыми. Во-вторых, требуется обеспечить устойчивость замкнутой системы. В-третьих, поскольку  может содержать множитель
может содержать множитель  в числителе (соответствующий интегрирующему звену), статический коэффициент усиления
в числителе (соответствующий интегрирующему звену), статический коэффициент усиления  может оказаться равным бесконечности. Поэтому нужно скорректировать процедуру выбора эталонного управляющего сигнала.
может оказаться равным бесконечности. Поэтому нужно скорректировать процедуру выбора эталонного управляющего сигнала.
Передаточная функция от входа 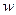 к ошибке
к ошибке  равна
равна
 , где
, где  ,
,
поэтому подынтегральное выражение в критерии качества будет зависеть от  , а не от
, а не от  . Чтобы обеспечить устойчивость получаемой оптимальной системы в общем случае нужно использовать параметризацию стабилизирующих регуляторов (см. аналогичную задачу при случайных возмущениях).
. Чтобы обеспечить устойчивость получаемой оптимальной системы в общем случае нужно использовать параметризацию стабилизирующих регуляторов (см. аналогичную задачу при случайных возмущениях).
При определении эталонного сигнала управления вроде бы все осталось по-прежнему: по теореме о предельном значении  .
.
Однако, проблема в том, что объект может содержать интегрирующие звенья, поэтому статический коэффициент усиления  обращается в бесконечность. В этом случае эталонный сигнал управления должен стремиться к нулю при
обращается в бесконечность. В этом случае эталонный сигнал управления должен стремиться к нулю при  . Например, можно принять
. Например, можно принять  при всех
при всех  .
.
Построим стандартную систему в задаче оптимизации по критерию
 .
.
Уравнения системы имеют вид
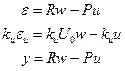
Учитывая, что первые два уравнения определяют ошибки по выходу и по управлению, имеем  ,
,  ,
,  и
и  . Как видим, все отличие от разомкнутой системы состоит в функции
. Как видим, все отличие от разомкнутой системы состоит в функции  , которая в данном случае не равна нулю и представляет собой передаточную функцию контура (без регулятора).
, которая в данном случае не равна нулю и представляет собой передаточную функцию контура (без регулятора).
Можно показать, что устойчивые полюса передаточной функции объекта  (и неустойчивые полюса, «отраженные» от мнимой оси) становятся корнями характеристического уравнения оптимальной замкнутой системы. Вроде бы получается, что для объекта, включающего интегрирующее звено, задача не имеет решения. Однако из этого правила есть исключение: если модель входного сигнала
(и неустойчивые полюса, «отраженные» от мнимой оси) становятся корнями характеристического уравнения оптимальной замкнутой системы. Вроде бы получается, что для объекта, включающего интегрирующее звено, задача не имеет решения. Однако из этого правила есть исключение: если модель входного сигнала  также содержит интегрирующее звено (например, для единичного ступенчатого сигнала
также содержит интегрирующее звено (например, для единичного ступенчатого сигнала  ), в ходе синтеза происходит сокращение двух множителей и оптимальная система оказывается устойчивой.
), в ходе синтеза происходит сокращение двух множителей и оптимальная система оказывается устойчивой.
Если учитывать динамику привода и датчиков, схема немного усложняется:

В этом случае стандартная система описывается матрицами
 ,
, 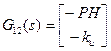 ,
,  и
и  .
.


 и объекта
и объекта  были устойчивыми. Во-вторых, требуется обеспечить устойчивость замкнутой системы. В-третьих, поскольку
были устойчивыми. Во-вторых, требуется обеспечить устойчивость замкнутой системы. В-третьих, поскольку  в числителе (соответствующий интегрирующему звену), статический коэффициент усиления
в числителе (соответствующий интегрирующему звену), статический коэффициент усиления  может оказаться равным бесконечности. Поэтому нужно скорректировать процедуру выбора эталонного управляющего сигнала.
может оказаться равным бесконечности. Поэтому нужно скорректировать процедуру выбора эталонного управляющего сигнала.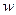 к ошибке
к ошибке  равна
равна , где
, где  ,
, , а не от
, а не от  .
. . Например, можно принять
. Например, можно принять  при всех
при всех  .
. .
.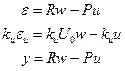
 ,
,  ,
,  и
и  . Как видим, все отличие от разомкнутой системы состоит в функции
. Как видим, все отличие от разомкнутой системы состоит в функции  , которая в данном случае не равна нулю и представляет собой передаточную функцию контура (без регулятора).
, которая в данном случае не равна нулю и представляет собой передаточную функцию контура (без регулятора). также содержит интегрирующее звено (например, для единичного ступенчатого сигнала
также содержит интегрирующее звено (например, для единичного ступенчатого сигнала  ), в ходе синтеза происходит сокращение двух множителей и оптимальная система оказывается устойчивой.
), в ходе синтеза происходит сокращение двух множителей и оптимальная система оказывается устойчивой.
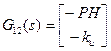 ,
,  .
.


