Теорема Парсеваля позволяет обнаружить связь между задачами анализа и синтеза при случайных (или стохастических) и детерминированных возмущениях.
Поскольку ошибка  стремится к нулю при
стремится к нулю при  , ее преобразование Лапласа
, ее преобразование Лапласа 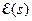 – устойчивая функция (все ее полюса имеют отрицательные вещественные части). Если рассматривать
– устойчивая функция (все ее полюса имеют отрицательные вещественные части). Если рассматривать 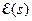 как передаточную функцию формирующего фильтра, то можно построить соответствующую спектральную плотность
как передаточную функцию формирующего фильтра, то можно построить соответствующую спектральную плотность 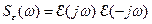 , так что
, так что  .
.
Таким образом, интеграл от квадрата функции  , стремящейся к нулю при
, стремящейся к нулю при  , равен среднему квадрату случайного процесса, имеющего спектральную плотность
, равен среднему квадрату случайного процесса, имеющего спектральную плотность  .
.
Пусть существует некоторая система с передаточной функцией  . Обозначим ее входной сигнал через
. Обозначим ее входной сигнал через 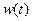 , а выходной – через
, а выходной – через  .
.

Если 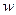 – единичный центрированный белый шум, то спектральная плотность выхода
– единичный центрированный белый шум, то спектральная плотность выхода  равна
равна  , а дисперсия выхода (средний квадрат) – интегралу от спектральной плотности по мнимой оси.
, а дисперсия выхода (средний квадрат) – интегралу от спектральной плотности по мнимой оси.
В то же время, если 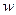 – единичный импульс (дельта-функция), изображение выхода по Лапласу равно
– единичный импульс (дельта-функция), изображение выхода по Лапласу равно  , а интегральная квадратическая ошибка равна тому же самому интегралу от
, а интегральная квадратическая ошибка равна тому же самому интегралу от  . Таким образом, вместо вычисления дисперсии выхода при белом шуме на входе можно вычислить интеграл от квадрата выходного сигнала при импульсном входе, и наоборот. Квадратный корень из этой величины называется
. Таким образом, вместо вычисления дисперсии выхода при белом шуме на входе можно вычислить интеграл от квадрата выходного сигнала при импульсном входе, и наоборот. Квадратный корень из этой величины называется  -нормой передаточной функции
-нормой передаточной функции  :
:
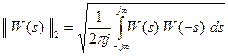
и вычисляется с помощью функции norm среды Matlab.
С другой стороны, пусть передаточная функция  зависит определенным образом от выбора регулятора
зависит определенным образом от выбора регулятора  . Тогда, как следует из сказанного, две следующие задачи оптимизации эквивалентны:
. Тогда, как следует из сказанного, две следующие задачи оптимизации эквивалентны:
1) найти регулятор  , минимизирующий дисперсию ошибки при единичном белом шуме на входе;
, минимизирующий дисперсию ошибки при единичном белом шуме на входе;
2) найти регулятор  , минимизирующий интегральную квадратическую ошибку при поступлении на вход единичного импульса (дельта-функции).
, минимизирующий интегральную квадратическую ошибку при поступлении на вход единичного импульса (дельта-функции).
Вторая задача в теории управления называется задачей  -оптимизации или просто
-оптимизации или просто  -задачей (поскольку требуется обеспечить минимум
-задачей (поскольку требуется обеспечить минимум  -нормы передаточной функции замкнутой системы), а о первой говорят как о стохастическом варианте
-нормы передаточной функции замкнутой системы), а о первой говорят как о стохастическом варианте  - задачи.
- задачи.

 стремится к нулю при
стремится к нулю при  , ее преобразование Лапласа
, ее преобразование Лапласа 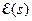 – устойчивая функция (все ее полюса имеют отрицательные вещественные части). Если рассматривать
– устойчивая функция (все ее полюса имеют отрицательные вещественные части). Если рассматривать 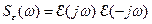 , так что
, так что  .
. .
. . Обозначим ее входной сигнал через
. Обозначим ее входной сигнал через 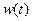 , а выходной – через
, а выходной – через 
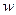 – единичный центрированный белый шум, то спектральная плотность выхода
– единичный центрированный белый шум, то спектральная плотность выхода  равна
равна  , а дисперсия выхода (средний квадрат) – интегралу от спектральной плотности по мнимой оси.
, а дисперсия выхода (средний квадрат) – интегралу от спектральной плотности по мнимой оси. , а интегральная квадратическая ошибка равна тому же самому интегралу от
, а интегральная квадратическая ошибка равна тому же самому интегралу от  . Таким образом, вместо вычисления дисперсии выхода при белом шуме на входе можно вычислить интеграл от квадрата выходного сигнала при импульсном входе, и наоборот. Квадратный корень из этой величины называется
. Таким образом, вместо вычисления дисперсии выхода при белом шуме на входе можно вычислить интеграл от квадрата выходного сигнала при импульсном входе, и наоборот. Квадратный корень из этой величины называется  -нормой передаточной функции
-нормой передаточной функции 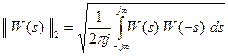
 . Тогда, как следует из сказанного, две следующие задачи оптимизации эквивалентны:
. Тогда, как следует из сказанного, две следующие задачи оптимизации эквивалентны:


