Чтобы понять особенности задачи, сначала мы рассмотрим простейшую разомкнутую систему, состоящую только из регулятора  и объекта
и объекта 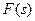 :
:

Входной сигнал  задан в виде преобразования Лапласа
задан в виде преобразования Лапласа  , так что его можно представить как результат прохождения единичного импульса (дельта-функции
, так что его можно представить как результат прохождения единичного импульса (дельта-функции 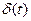 ) через звено с передаточной функцией
) через звено с передаточной функцией  . Такой способ общепринят при моделировании входных сигналов и позволяет представить систему в стандартном виде: на входе – дельта-функция, на выходе – ошибка.
. Такой способ общепринят при моделировании входных сигналов и позволяет представить систему в стандартном виде: на входе – дельта-функция, на выходе – ошибка.
Передаточная функция системы от входа 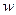 к выходу
к выходу  равна
равна  .
.
Предполагается, что все звенья устойчивы. Это значит, что все полюса функций  и
и  имеют отрицательные вещественные части и регулятор
имеют отрицательные вещественные части и регулятор  , который требуется найти, также должен обладать этим свойством. Кроме того, регулятор должен обеспечить минимум интегральной квадратической ошибки
, который требуется найти, также должен обладать этим свойством. Кроме того, регулятор должен обеспечить минимум интегральной квадратической ошибки  , где
, где  . Подынтегральное выражение имеет форму Ошибка! Источник ссылки не найден., как для задачи Винера, поэтому можно применить уже известный алгоритм поиска оптимальной устойчивой передаточной функции
. Подынтегральное выражение имеет форму Ошибка! Источник ссылки не найден., как для задачи Винера, поэтому можно применить уже известный алгоритм поиска оптимальной устойчивой передаточной функции  .
.
Попытаемся понять, какие результаты мы можем получить в результате оптимизации. Прежде всего, выбор регулятора из условия  сразу дает
сразу дает  , то есть, ошибка будет нулевой не только при ступенчатом, но и при любом другом входе. Это так называемое условие инвариантности, при котором обеспечивается идеальное слежение за эталонным сигналом. Именно такой регулятор будет получен в результате оптимизации «в лоб».
, то есть, ошибка будет нулевой не только при ступенчатом, но и при любом другом входе. Это так называемое условие инвариантности, при котором обеспечивается идеальное слежение за эталонным сигналом. Именно такой регулятор будет получен в результате оптимизации «в лоб».
К сожалению, все не так просто. Как правило, передаточные функции реальных объектов – строго правильные, то есть, степень их числителя меньше, чем степень знаменателя. Тогда передаточная функция регулятора  будет неправильной (степень числителя больше степени знаменателя). Как было показано при анализе задачи оптимизации при случайных возмущениях, такой регулятор неприменим в практических задачах по двум причинам:
будет неправильной (степень числителя больше степени знаменателя). Как было показано при анализе задачи оптимизации при случайных возмущениях, такой регулятор неприменим в практических задачах по двум причинам:
1) регулятор содержит дифференцирующее звено, поэтому при скачкообразном изменении входного сигнала сигнал управления должен теоретически стать бесконечным;
2) регулятор усиливает высокочастотные помехи измерений вместо того, чтобы подавлять их; это делает систему неработоспособной.
В задаче оптимизации при случайных возмущениях мы добивались «ската» частотной характеристики регулятора на высоких частотах с помощью ограничения на сигнал управления: в критерий качества вводилась дисперсия управления с некоторым весовым коэффициентом, который подстраивался методом проб и ошибок.
Если формально составить критерий  , добавив интеграл от квадрата сигнала управления
, добавив интеграл от квадрата сигнала управления  с весовым коэффициентом
с весовым коэффициентом 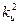 , то ничего хорошего не получится, поскольку установившееся значение
, то ничего хорошего не получится, поскольку установившееся значение  при
при  не равно нулю. Следовательно, интеграл расходится и теорема Парсеваля неприменима. Оптимизация в частотной области не имеет смысла: если формально применить алгоритм синтеза, получится регулятор, для которого ошибка в установившемся режиме (при
не равно нулю. Следовательно, интеграл расходится и теорема Парсеваля неприменима. Оптимизация в частотной области не имеет смысла: если формально применить алгоритм синтеза, получится регулятор, для которого ошибка в установившемся режиме (при  ) не равна нулю.
) не равна нулю.
Чтобы грамотно ограничить управляющий сигнал, нужно ввести ошибку управления  , то есть отклонение фактического сигнала управления
, то есть отклонение фактического сигнала управления  от некоторого эталонного сигнала
от некоторого эталонного сигнала  , который должен быть выбран так, чтобы функция
, который должен быть выбран так, чтобы функция  стремилась к нулю при
стремилась к нулю при  . Тогда можно искать минимум критерия
. Тогда можно искать минимум критерия  ,
,
это позволит ограничить мощность управления и при этом минимизировать ошибку слежения. Изменяя коэффициент  , мы получим семейство Парето-оптимальных регуляторов, как и в задаче оптимизации при случайных возмущениях.
, мы получим семейство Парето-оптимальных регуляторов, как и в задаче оптимизации при случайных возмущениях.
Как же выбрать сигнал  ? Для простоты рассмотрим только случай ступенчатого входного сигнала. Поскольку передаточная функция
? Для простоты рассмотрим только случай ступенчатого входного сигнала. Поскольку передаточная функция  устойчива, установившееся значение
устойчива, установившееся значение  сигнала
сигнала  при
при  – постоянная величина, ее можно рассчитать следующим образом.
– постоянная величина, ее можно рассчитать следующим образом.
Если вход 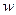 – это единичный импульс, то установившееся значение эталонного сигнала
– это единичный импульс, то установившееся значение эталонного сигнала  можно определить по теореме о конечном значении для преобразования Лапласа
можно определить по теореме о конечном значении для преобразования Лапласа  .
.
Например, если  – единичный ступенчатый сигнал, для которого
– единичный ступенчатый сигнал, для которого  , то
, то  . С другой стороны, для того, чтобы установившаяся ошибка была равна нулю, необходимо, чтобы предельное значение сигнала
. С другой стороны, для того, чтобы установившаяся ошибка была равна нулю, необходимо, чтобы предельное значение сигнала  тоже было равно
тоже было равно  . Учитывая, что
. Учитывая, что  – устойчивая передаточная функция, имеем
– устойчивая передаточная функция, имеем  , где
, где  – нужное нам установившееся значение сигнала управления, а
– нужное нам установившееся значение сигнала управления, а  – статический коэффициент усиления объекта, который вычисляется по формуле
– статический коэффициент усиления объекта, который вычисляется по формуле  (в среде Matlab это делает функция dcgain). Таким образом, в качестве эталонного сигнала управления можно выбрать любой сигнал
(в среде Matlab это делает функция dcgain). Таким образом, в качестве эталонного сигнала управления можно выбрать любой сигнал  , у которого предельное значение при
, у которого предельное значение при  равно
равно 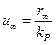 , например, ступенчатый сигнал
, например, ступенчатый сигнал  , изображение которого равно
, изображение которого равно  .
.
Теперь построим стандартную систему, соответствующую задаче оптимизации. Уравнения в изображениях имеют вид:
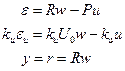
Учитывая, что первые два уравнения определяют ошибки по выходу и по управлению, имеем  ,
,  ,
,  и
и  .
.

 и объекта
и объекта 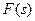 :
:
 задан в виде преобразования Лапласа
задан в виде преобразования Лапласа  , так что его можно представить как результат прохождения единичного импульса (дельта-функции
, так что его можно представить как результат прохождения единичного импульса (дельта-функции 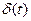 ) через звено с передаточной функцией
) через звено с передаточной функцией 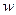 к выходу
к выходу  равна
равна  .
. и
и  , где
, где  . Подынтегральное выражение имеет форму Ошибка! Источник ссылки не найден., как для задачи Винера, поэтому можно применить уже известный алгоритм поиска оптимальной устойчивой передаточной функции
. Подынтегральное выражение имеет форму Ошибка! Источник ссылки не найден., как для задачи Винера, поэтому можно применить уже известный алгоритм поиска оптимальной устойчивой передаточной функции  сразу дает
сразу дает  , то есть, ошибка будет нулевой не только при ступенчатом, но и при любом другом входе. Это так называемое условие инвариантности, при котором обеспечивается идеальное слежение за эталонным сигналом. Именно такой регулятор будет получен в результате оптимизации «в лоб».
, то есть, ошибка будет нулевой не только при ступенчатом, но и при любом другом входе. Это так называемое условие инвариантности, при котором обеспечивается идеальное слежение за эталонным сигналом. Именно такой регулятор будет получен в результате оптимизации «в лоб». будет неправильной (степень числителя больше степени знаменателя). Как было показано при анализе задачи оптимизации при случайных возмущениях, такой регулятор неприменим в практических задачах по двум причинам:
будет неправильной (степень числителя больше степени знаменателя). Как было показано при анализе задачи оптимизации при случайных возмущениях, такой регулятор неприменим в практических задачах по двум причинам: , добавив интеграл от квадрата сигнала управления
, добавив интеграл от квадрата сигнала управления  с весовым коэффициентом
с весовым коэффициентом 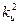 , то ничего хорошего не получится, поскольку установившееся значение
, то ничего хорошего не получится, поскольку установившееся значение  не равно нулю. Следовательно, интеграл расходится и теорема Парсеваля неприменима. Оптимизация в частотной области не имеет смысла: если формально применить алгоритм синтеза, получится регулятор, для которого ошибка в установившемся режиме (при
не равно нулю. Следовательно, интеграл расходится и теорема Парсеваля неприменима. Оптимизация в частотной области не имеет смысла: если формально применить алгоритм синтеза, получится регулятор, для которого ошибка в установившемся режиме (при  , то есть отклонение фактического сигнала управления
, то есть отклонение фактического сигнала управления  , который должен быть выбран так, чтобы функция
, который должен быть выбран так, чтобы функция  стремилась к нулю при
стремилась к нулю при  ,
, , мы получим семейство Парето-оптимальных регуляторов, как и в задаче оптимизации при случайных возмущениях.
, мы получим семейство Парето-оптимальных регуляторов, как и в задаче оптимизации при случайных возмущениях. сигнала
сигнала  можно определить по теореме о конечном значении для преобразования Лапласа
можно определить по теореме о конечном значении для преобразования Лапласа  .
. , то
, то  . С другой стороны, для того, чтобы установившаяся ошибка была равна нулю, необходимо, чтобы предельное значение сигнала
. С другой стороны, для того, чтобы установившаяся ошибка была равна нулю, необходимо, чтобы предельное значение сигнала  тоже было равно
тоже было равно  . Учитывая, что
. Учитывая, что  , где
, где  – статический коэффициент усиления объекта, который вычисляется по формуле
– статический коэффициент усиления объекта, который вычисляется по формуле  (в среде Matlab это делает функция dcgain). Таким образом, в качестве эталонного сигнала управления можно выбрать любой сигнал
(в среде Matlab это делает функция dcgain). Таким образом, в качестве эталонного сигнала управления можно выбрать любой сигнал 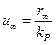 , например, ступенчатый сигнал
, например, ступенчатый сигнал  , изображение которого равно
, изображение которого равно  .
.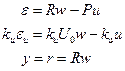
 ,
,  ,
,  и
и  .
.


