Инструкция по выполнению работы. Основная часть команд вводится в командном окне среды Matlab
Основная часть команд вводится в командном окне среды Matlab. Команды, которые надо применять в других окнах, обозначены иконками соответствующих программ.
| Этап выполнения задания
| Команды и иллюстрации
| | 1. Создайте новый m-файл (скрипт) с командами, которые строят модели объекта и входного сигнала:
clear all;
P = tf (1, [1 1]); % объект
R = tf (1, [1 0]); % модель входного сигнала
| | 2. Постройте стандартную систему и найдите оптимальный регулятор без ограничений на управление с помощью функции h2opt (файл h2opt.m нужно скопировать в рабочую папку):
sys = [ R -P
R 0];
C = h2opt (sys)
Запустите скрипт, нажав (F5).
| | 3. Постройте частотную характеристику полученного регулятора и сделайте выводы.
| bode (C)
| 4. Добавьте в скрипт (в нужное место!) команды для определения установившегося значения сигнала управления  и изображения по Лапласу эталонного управляющего сигнала  :
uInf = dcgain(tf([1 0],1)*R/P);
U0 = uInf*tf(1, [1 0]);
| | 5. Измените стандартную систему с учетом ограничения на мощность сигнала управления
kU = 1;
sys = [ R -P
kU*U0 -kU
R 0];
Снова запустите скрипт (постройте оптимальный регулятор) и постройте частотную характеристику полученного регулятора. Сравните с предыдущим вариантом.
| 6. Запустите Simulink, соберите модель, как показано на рисунке, и сохраните ее под именем lab7sim1.mdl.
Для того, чтобы вывести на осциллограф два сигнала, используйте мультиплексор (блок Mux, группа Singal Routing).
| 7. Установите параметры блоков, как показано на рисунках:
Step Signal Controller Plant
   
Обратите внимание, что в числитель блока Signal добавлен множитель  , поскольку входной сигнал – это единичная ступенька, а не дельта-функция.
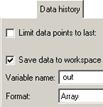
| | 8. В параметрах осциллографа снимите флажок Limit data points (ограничивать число запоминаемых точек) и установите режим сохранения данных (Save data to workspace) в виде массива (Array) с именем out.
| 
| | 9. Добавьте в конец скрипта команды для построения числителей и знаменателей отдельных блоков
[nP,dP] = tfdata(P, 'v');
[nR,dR] = tfdata(R, 'v');
[nC,dC] = tfdata(C, 'v');
а также для запуска моделирования
sim('lab7sim1');
и построения графиков
figure(1);
plot(out(:,1), out(:,2), out(:,1), out(:,3));
| | 10. Запустите скрипт и перенесите полученный график в отчет.
| 11. Повторите расчеты при  и  . Сделайте выводы. Закройте файлы (скрипт и модель).
| | 12. Теперь будем исследовать замкнутую систему управления судном по курсу. Создайте новый скрипт и добавьте в него команды для построения моделей судна, привода, измерительной системы и входного ступенчатого сигнала:
clear all;
P = tf (0.0694, [18.2 1 0]); % модель судна
H = tf (1, [2 1]); % привод
G = tf (1, [6 1]); % обратная связь
R = tf (1, [1 0]); % модель сигнала
| | 13. Добавьте команды для подготовки данных к моделированию
[nP,dP] = tfdata(P, 'v');
[nR,dR] = tfdata(R, 'v');
[nH,dH] = tfdata(H, 'v');
[nG,dG] = tfdata(G, 'v');
| | 14. Найдите передаточную функцию оптимального регулятора без учета ограничений на управление:
sys = [ R -P*H
R -P*H*G];
[C,Poles] = h2opt (sys)
| | 15. Постройте частотную характеристику полученного регулятора и сделайте выводы.
| bode (C)
| | 16. Постройте оптимальный регулятор с ограничением на управление (учитывая, что установившееся значение сигнала управления для объекта с интегратором равно нулю):
kU = 1;
sys = [ R -P*H
0 -kU
R -P*H*G];
[C,Poles] = h2opt (sys)
Приведите в отчете его передаточную функцию и частотную характеристику. Сделайте выводы.
| 17. Запустите Simulink, соберите модель, как показано на рисунке, и сохраните ее под именем lab7sim.mdl.
Для того, чтобы вывести на осциллограф два сигнала, используйте мультиплексор (блок Mux, группа Singal Routing).
| 18. Установите параметры блоков, как показано на рисунках:
Step Signal Controller Actuator Plant Measurement
     
Обратите внимание, что в числитель блока Signal добавлен множитель , поскольку входной сигнал – это единичная ступенька, а не дельта-функция.
| | 19. В параметрах осциллографа снимите флажок Limit data points (ограничивать число запоминаемых точек) и установите режим сохранения данных (Save data to workspace) в виде массива (Array) с именем out. Аналогично для осциллографа Control установите вывод данных в массив u.
| 
| | 20. Добавьте в скрипт команды для выполнения моделирования
[nC,dC] = tfdata(C, 'v');
sim('lab7sim');
построения графика (эталонный и фактический переходные процессы):
figure(1);
plot(out(:,1), out(:,2), out(:,1), out(:,3));
и расчета интегральных квадратических ошибок по выходу и по управлению (интегрирование методом трапеций, функция trapz):
uInf = 0; % установившееся значение управления
err2 = (out(:,2)-out(:,3)).^2; % квадрат ошибки
errOpt = trapz(out(:,1),err2) % интегральная кв. ошибка
errU2 = (u(:,2) - uInf).^2; % квадрат ошибки по управлению
errU = trapz(u(:,1),errU2) % интегральная кв. ошибка
| | 21. Установите время моделирования 100 с (меню Simulation-Simulation parameters-Stop time). Запустите скрипт и скопируйте в отчет полученный график.
| | 22. Измените скрипт так, чтобы построить кривую качества системы (зависимость интегральный квадратических ошибок по выходу и управлению для Парето-оптимальных регуляторов):
kU = [0.2 0.25 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.2 1.5 1.7 2];
uInf = 0; % установившееся значение управления
errOut = []; % освободить массивы
errU = [];
for i=1:length(kU)
fprintf('\n%g', kU(i)); % вывод текущего kU
sys = [ R -P % стандартная система
0 -kU(i)
R -P];
[C,Poles] = h2opt (sys); % синтез оптимального регулятора
[nC,dC] = tfdata(C, 'v');
sim('lab7sim'); % моделирование
err2 = (out(:,2)-out(:,3)).^2;
u2 = (u(:,2) - uInf).^2;
errOut(i) = trapz(out(:,1),err2);
errU(i) = trapz(u(:,1),u2);
end;
| | 23. После цикла добавьте команды для построения кривой качества
figure(1);
plot(errOut, errU, '-o');
xlabel('Error');
ylabel('Control error');
| | 24. Запустите скрипт на выполнение. Скопируйте в отчет полученную кривую качества. Сделайте выводы.
| | | | | |
Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|
Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Устройство рабочих органов мясорубки Независимо от марки мясорубки и её технических характеристик, все они имеют принципиально одинаковые устройства...
Ведение учета результатов боевой подготовки в роте и во взводе Содержание журнала учета боевой подготовки во взводе. Учет результатов боевой подготовки - есть отражение количественных и качественных показателей выполнения планов подготовки соединений...
Сравнительно-исторический метод в языкознании сравнительно-исторический метод в языкознании является одним из основных и представляет собой совокупность приёмов...
|
Огоньки» в основной период В основной период смены могут проводиться три вида «огоньков»: «огонек-анализ», тематический «огонек» и «конфликтный» огонек...
Упражнение Джеффа. Это список вопросов или утверждений, отвечая на которые участник может раскрыть свой внутренний мир перед другими участниками и узнать о других участниках больше...
Влияние первой русской революции 1905-1907 гг. на Казахстан. Революция в России (1905-1907 гг.), дала первый толчок политическому пробуждению трудящихся Казахстана, развитию национально-освободительного рабочего движения против гнета. В Казахстане, находившемся далеко от политических центров Российской империи...
|
|
