Теорема Парсеваля
Для большинства задач в теории управления существует два типа решений – временное (когда рассматривается изменение сигналов во времени) и частотный (работа с передаточными функциями и частотными характеристиками). Эти подходы не исключают, а взаимно дополняют друг друга, позволяя увидеть разные стороны одной задачи. Для построения оптимального фильтра Винера мы использовали операции с передаточными функциями (частотный метод Боде и Шеннона), хотя сам Винер впервые предложил решение этой задачи с помощью временного метода (на основе корреляционных функций). Для того, чтобы использовать уже рассмотренные алгоритмы, нужно «перевести» задачу с критерием (13) в частотную область, то есть, выразить критерий через изображения сигналов по Лапласу и передаточные функции. Это позволяет сделать теорема Парсеваля, которая утверждает, что интеграл от квадрата функции (14) Выражение Заметим, что функционал (14) в нашей задаче (при известном входном сигнале) совпадает по форме (при
|
, которая равна нулю при 
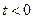и стремится к нулю при 
, равен интегралу от «квадрата» ее преобразования Лапласа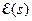 
: 
.
можно назвать «квадратом» потому что оно на мнимой оси (где берется интеграл), при подстановке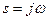 
, действительно является квадратом частотной характеристики 
: 
.
) с функционалом Ошибка! Источник ссылки не найден., который получен в задаче фильтрации при случайных возмущениях. Поэтому для решения задачи можно использовать алгоритм, применявшийся при расчете фильтра Винера.
