Изложим на примере четырех сходящихся сил, приложенных в точке  (рис.1.9), два способа сложения сил: векторный и аналитический. При векторном способе сложения сходящихся сил (его называют также геометрическим способом) равнодействующая
(рис.1.9), два способа сложения сил: векторный и аналитический. При векторном способе сложения сходящихся сил (его называют также геометрическим способом) равнодействующая 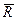 системы сил приложена в той же точке О и является замыкающей стороной силового многоугольника, построенного на слагаемых силах (рис. 1.10):
системы сил приложена в той же точке О и является замыкающей стороной силового многоугольника, построенного на слагаемых силах (рис. 1.10):  или
или  .
.
При построении силового многоугольника надо к концу первого слагаемого вектора

присоединить параллельно перенесенный вектор

, затем присоединить к концу вектора

параллельно перенесенный вектор

и т.д. Векторный способ сложения сходящихся векторов является простым и наглядным. Однако точность определения равнодействующей силы
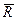
зависит от точности построения силового многоугольника.
На практике чаще применяют аналитический способ сложения сходящихся сил, который называют способом проекций. Спроектируем силы  на горизонтальную ось и алгебраически сложим их проекции:
на горизонтальную ось и алгебраически сложим их проекции:
 .
.
Проекцией равнодействующей 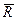 сходящихся сил
сходящихся сил  на горизонтальную ось будет отрезок od.
на горизонтальную ось будет отрезок od.
Обобщая эти способы сложения сходящихся сил для плоской системы n сил, и обозначив проекции равнодействующей на оси координат через  можно написать равенства в векторном виде и в проекциях на оси координат:
можно написать равенства в векторном виде и в проекциях на оси координат:
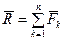 ,
,  ,
,  . (1.1)
. (1.1)
Модуль равнодействующей определим через ее проекции на координатные оси:  . Направление равнодействующей определяется через ее направляющие косинусы:
. Направление равнодействующей определяется через ее направляющие косинусы:
 ,
,  .
.
В случае равновесия системы сходящихся сил равнодействующая  . Ее модуль
. Ее модуль 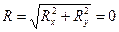 , следовательно
, следовательно
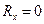 ,
,  . (1.2)
. (1.2)
Учитывая равенства (1.1) и (1.2), получим уравнения равновесия плоской системы сходящихся сил:
 ,
,  . (1.3)
. (1.3)
Таким образом, для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на оси координат.
Момент силы относительно центра (точки)
Пусть на тело в точке А действует сила  (рис. 1.11). Из некоторого центра О проведем радиус-вектор
(рис. 1.11). Из некоторого центра О проведем радиус-вектор  . Моментом силы
. Моментом силы  относительно центра
относительно центра  называется вектор, равный векторному произведению радиус-вектора
называется вектор, равный векторному произведению радиус-вектора 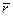 , проведенного из центра
, проведенного из центра  в точку
в точку 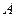 , где приложена сила, на вектор силы
, где приложена сила, на вектор силы  :
:
 . (1.4)
. (1.4)
 Из определения векторного произведения следует, что вектор
Из определения векторного произведения следует, что вектор 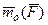 направлен перпендикулярно плоскости ΔОАВ, образованной векторами
направлен перпендикулярно плоскости ΔОАВ, образованной векторами 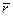 и
и  , в ту сторону, откуда мы видим направление силы
, в ту сторону, откуда мы видим направление силы  против хода часовой стрелки. Модуль вектора момента равен
против хода часовой стрелки. Модуль вектора момента равен
 ,
,
где  – плечо силы
– плечо силы  относительно центра
относительно центра  , т.е. кратчайшее расстояние от центра
, т.е. кратчайшее расстояние от центра  до линии действия силы
до линии действия силы  .
.
Наряду с определением момента силы относительно центра (как вектор) сформулируем определение момента силы относительно точки (как алгебраическая величина).
Момент силы  относительно точки
относительно точки  есть взятое со знаком плюс или минус произведение модуля силы на кратчайшее расстояние от точки
есть взятое со знаком плюс или минус произведение модуля силы на кратчайшее расстояние от точки  до линии действия силы:
до линии действия силы:
 . (1.5)
. (1.5)
Момент силы измеряется Ньютон-метрами (Н·м). Алгебраическая величина момента силы  изображается в виде дуговой стрелки (рис. 1.11). Момент является положительным, если сила стремится повернуть тело относительно точки против хода часовой стрелки. Отметим два свойства момента силы относительно точки. Момент силы относительно точки не изменится, если силу как скользящий вектор перенести вдоль линии действия. Например, если точку приложения А силы
изображается в виде дуговой стрелки (рис. 1.11). Момент является положительным, если сила стремится повернуть тело относительно точки против хода часовой стрелки. Отметим два свойства момента силы относительно точки. Момент силы относительно точки не изменится, если силу как скользящий вектор перенести вдоль линии действия. Например, если точку приложения А силы  перенести в точку С (рис. 1.11). Момент силы относительно точки равняется нулю, если точка лежит на линии действия этой силы. В этом случае плечо h равно нулю.
перенести в точку С (рис. 1.11). Момент силы относительно точки равняется нулю, если точка лежит на линии действия этой силы. В этом случае плечо h равно нулю.
 присоединить параллельно перенесенный вектор
присоединить параллельно перенесенный вектор  , затем присоединить к концу вектора
, затем присоединить к концу вектора  параллельно перенесенный вектор
параллельно перенесенный вектор  и т.д. Векторный способ сложения сходящихся векторов является простым и наглядным. Однако точность определения равнодействующей силы
и т.д. Векторный способ сложения сходящихся векторов является простым и наглядным. Однако точность определения равнодействующей силы 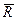 зависит от точности построения силового многоугольника.
зависит от точности построения силового многоугольника.

 (рис.1.9), два способа сложения сил: векторный и аналитический. При векторном способе сложения сходящихся сил (его называют также геометрическим способом) равнодействующая
(рис.1.9), два способа сложения сил: векторный и аналитический. При векторном способе сложения сходящихся сил (его называют также геометрическим способом) равнодействующая  или
или  .
.
 на горизонтальную ось и алгебраически сложим их проекции:
на горизонтальную ось и алгебраически сложим их проекции: .
. можно написать равенства в векторном виде и в проекциях на оси координат:
можно написать равенства в векторном виде и в проекциях на оси координат: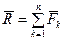 ,
,  ,
,  . (1.1)
. (1.1) . Направление равнодействующей определяется через ее направляющие косинусы:
. Направление равнодействующей определяется через ее направляющие косинусы: ,
,  .
. . Ее модуль
. Ее модуль 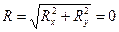 , следовательно
, следовательно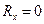 ,
,  . (1.2)
. (1.2) ,
,  . (1.3)
. (1.3) (рис. 1.11). Из некоторого центра О проведем радиус-вектор
(рис. 1.11). Из некоторого центра О проведем радиус-вектор  . Моментом силы
. Моментом силы 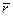 , проведенного из центра
, проведенного из центра 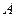 , где приложена сила, на вектор силы
, где приложена сила, на вектор силы  . (1.4)
. (1.4) Из определения векторного произведения следует, что вектор
Из определения векторного произведения следует, что вектор 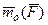 направлен перпендикулярно плоскости ΔОАВ, образованной векторами
направлен перпендикулярно плоскости ΔОАВ, образованной векторами  ,
, – плечо силы
– плечо силы  . (1.5)
. (1.5) изображается в виде дуговой стрелки (рис. 1.11). Момент является положительным, если сила стремится повернуть тело относительно точки против хода часовой стрелки. Отметим два свойства момента силы относительно точки. Момент силы относительно точки не изменится, если силу как скользящий вектор перенести вдоль линии действия. Например, если точку приложения А силы
изображается в виде дуговой стрелки (рис. 1.11). Момент является положительным, если сила стремится повернуть тело относительно точки против хода часовой стрелки. Отметим два свойства момента силы относительно точки. Момент силы относительно точки не изменится, если силу как скользящий вектор перенести вдоль линии действия. Например, если точку приложения А силы 


