Рассмотрим движение точки 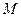 одновременно по отношению к двум системам отсчета, из которых одна система
одновременно по отношению к двум системам отсчета, из которых одна система  считается основной или условно неподвижной, а другая система
считается основной или условно неподвижной, а другая система  некоторым образом движется по отношению к первой (рис. 2.16). Каждая из этих систем отсчета связана, конечно, с определенным телом, которое на чертеже, как правило, не показывают. Введем следующие определения.
некоторым образом движется по отношению к первой (рис. 2.16). Каждая из этих систем отсчета связана, конечно, с определенным телом, которое на чертеже, как правило, не показывают. Введем следующие определения.
Движение, совершаемое точкой 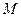 по отношению к подвижной системе отсчета
по отношению к подвижной системе отсчета  , называется относительным. Например, движение падающего мячика с полки в движущемся поезде. В этом случае оси
, называется относительным. Например, движение падающего мячика с полки в движущемся поезде. В этом случае оси  связывают с вагоном.
связывают с вагоном.
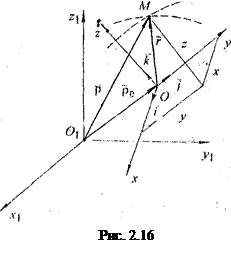
Траекторию, скорость и ускорение точки 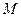 при таком движении (движение мячика относительно вагона) называют относительными. Закон относительного движения точки можно задать законом изменения радиус-вектора
при таком движении (движение мячика относительно вагона) называют относительными. Закон относительного движения точки можно задать законом изменения радиус-вектора  . Соответственно траектория, скорость
. Соответственно траектория, скорость  , и ускорение
, и ускорение  точки в ее движении относительно подвижной системы координат называются относительными. Для определения относительной скорости и относительного ускорения точки следует мысленно остановить движение подвижной системы координат и вычислить их по правилам кинематики точки.
точки в ее движении относительно подвижной системы координат называются относительными. Для определения относительной скорости и относительного ускорения точки следует мысленно остановить движение подвижной системы координат и вычислить их по правилам кинематики точки.
Движение подвижной системы координат  относительно неподвижной
относительно неподвижной  называют переносным движением (в том же примере, движение вагона поезда относительно условно неподвижной Земли). Переносной скоростью
называют переносным движением (в том же примере, движение вагона поезда относительно условно неподвижной Земли). Переносной скоростью  и переносным ускорением
и переносным ускорением  точки М в данный момент времени называют векторы, равные соответственно скорости
точки М в данный момент времени называют векторы, равные соответственно скорости  и ускорению
и ускорению  той точки т подвижной системы координат, с которой совпадает в данный момент движущаяся точка М. Для определения переносной скорости
той точки т подвижной системы координат, с которой совпадает в данный момент движущаяся точка М. Для определения переносной скорости  и переносного ускорения
и переносного ускорения  в данный момент времени необходимо мысленно остановить в этот момент времени относительное движение точки, определить положение точки т тела, неизменно связанной с подвижной системой координат, где находится в остановленный момент точка М, и вычислить скорость и ускорение точки т тела, совершающего переносное движение относительно неподвижной системы координат.
в данный момент времени необходимо мысленно остановить в этот момент времени относительное движение точки, определить положение точки т тела, неизменно связанной с подвижной системой координат, где находится в остановленный момент точка М, и вычислить скорость и ускорение точки т тела, совершающего переносное движение относительно неподвижной системы координат.
Движение точки М относительно неподвижной системы координат называют абсолютным или сложным. Соответственно, траекторию, скорость  и ускорение
и ускорение  относительно неподвижной системы координат называют абсолютными.
относительно неподвижной системы координат называют абсолютными.
Абсолютная скорость точки  определяется по теореме о сложении скоростей, согласно которой абсолютная скорость точки, совершающей сложное движение, равна векторной сумме переносной и относительной скоростей:
определяется по теореме о сложении скоростей, согласно которой абсолютная скорость точки, совершающей сложное движение, равна векторной сумме переносной и относительной скоростей:
 (2.32)
(2.32)
Абсолютное ускорение точки  определяется по теореме Кориолиса, согласно которой абсолютное ускорение точки, совершающей сложное движение, равно геометрической сумме переносного, относительного и Кориолисова ускорений:
определяется по теореме Кориолиса, согласно которой абсолютное ускорение точки, совершающей сложное движение, равно геометрической сумме переносного, относительного и Кориолисова ускорений:
 . (2.33)
. (2.33)
Кориолисово ускорение характеризует изменение относительной скорости точки при переносном движении и изменение переносной скорости точки при ее относительном движении. Оно равно удвоенному векторному произведению
 , (2.34)
, (2.34)
 где
где  - вектор угловой скорости переносного движения,
- вектор угловой скорости переносного движения,  - вектор относительной скорости точки. Направление вектора Кориолисова ускорения определяется по правилу векторного произведения: Кориолисово ускорение будет направлено, перпендикулярно плоскости, в которой лежат векторы
- вектор относительной скорости точки. Направление вектора Кориолисова ускорения определяется по правилу векторного произведения: Кориолисово ускорение будет направлено, перпендикулярно плоскости, в которой лежат векторы  и
и  (рис. 2.17), в ту сторону, откуда кратчайший поворот от вектора
(рис. 2.17), в ту сторону, откуда кратчайший поворот от вектора  к вектору
к вектору  видится происходящим против хода часовой стрелки.
видится происходящим против хода часовой стрелки.
Модуль Кориолисова ускорения равен  . Кориолисово ускорение равно нулю в трех случаях: переносное движение тела является поступательным (
. Кориолисово ускорение равно нулю в трех случаях: переносное движение тела является поступательным ( ), относительная скорость точки в данный момент времени равна нулю (
), относительная скорость точки в данный момент времени равна нулю ( ), векторы переносной угловой скорости и вектор относительной скорости параллельны (
), векторы переносной угловой скорости и вектор относительной скорости параллельны ( ).
).

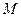 одновременно по отношению к двум системам отсчета, из которых одна система
одновременно по отношению к двум системам отсчета, из которых одна система  считается основной или условно неподвижной, а другая система
считается основной или условно неподвижной, а другая система  некоторым образом движется по отношению к первой (рис. 2.16). Каждая из этих систем отсчета связана, конечно, с определенным телом, которое на чертеже, как правило, не показывают. Введем следующие определения.
некоторым образом движется по отношению к первой (рис. 2.16). Каждая из этих систем отсчета связана, конечно, с определенным телом, которое на чертеже, как правило, не показывают. Введем следующие определения.
 . Соответственно траектория, скорость
. Соответственно траектория, скорость  , и ускорение
, и ускорение  точки в ее движении относительно подвижной системы координат называются относительными. Для определения относительной скорости и относительного ускорения точки следует мысленно остановить движение подвижной системы координат и вычислить их по правилам кинематики точки.
точки в ее движении относительно подвижной системы координат называются относительными. Для определения относительной скорости и относительного ускорения точки следует мысленно остановить движение подвижной системы координат и вычислить их по правилам кинематики точки. и переносным ускорением
и переносным ускорением  точки М в данный момент времени называют векторы, равные соответственно скорости
точки М в данный момент времени называют векторы, равные соответственно скорости  и ускорению
и ускорению  той точки т подвижной системы координат, с которой совпадает в данный момент движущаяся точка М. Для определения переносной скорости
той точки т подвижной системы координат, с которой совпадает в данный момент движущаяся точка М. Для определения переносной скорости  в данный момент времени необходимо мысленно остановить в этот момент времени относительное движение точки, определить положение точки т тела, неизменно связанной с подвижной системой координат, где находится в остановленный момент точка М, и вычислить скорость и ускорение точки т тела, совершающего переносное движение относительно неподвижной системы координат.
в данный момент времени необходимо мысленно остановить в этот момент времени относительное движение точки, определить положение точки т тела, неизменно связанной с подвижной системой координат, где находится в остановленный момент точка М, и вычислить скорость и ускорение точки т тела, совершающего переносное движение относительно неподвижной системы координат. и ускорение
и ускорение  относительно неподвижной системы координат называют абсолютными.
относительно неподвижной системы координат называют абсолютными. (2.32)
(2.32) . (2.33)
. (2.33) , (2.34)
, (2.34) где
где  - вектор угловой скорости переносного движения,
- вектор угловой скорости переносного движения,  - вектор относительной скорости точки. Направление вектора Кориолисова ускорения определяется по правилу векторного произведения: Кориолисово ускорение будет направлено, перпендикулярно плоскости, в которой лежат векторы
- вектор относительной скорости точки. Направление вектора Кориолисова ускорения определяется по правилу векторного произведения: Кориолисово ускорение будет направлено, перпендикулярно плоскости, в которой лежат векторы  . Кориолисово ускорение равно нулю в трех случаях: переносное движение тела является поступательным (
. Кориолисово ускорение равно нулю в трех случаях: переносное движение тела является поступательным ( ), относительная скорость точки в данный момент времени равна нулю (
), относительная скорость точки в данный момент времени равна нулю ( ), векторы переносной угловой скорости и вектор относительной скорости параллельны (
), векторы переносной угловой скорости и вектор относительной скорости параллельны ( ).
).


