Законы динамики
Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил. Материальными объектами в динамике являются материальная точка (точка, обладающая массой), абсолютно твердое тело и механическая система материальных точек или тел. При изучении движения тел в динамике, в отличие от кинематики, принимают во внимание как действующие на них силы, так и инертность самих материальных тел. Количественной мерой инертности тела при поступательном движении является масса Первый закон динамики (закон инерции). Материальная точка, изолированная от действия каких-либо других материальных тел, сохраняет относительно неподвижной системы отсчета состояние покоя или равномерного прямолинейного движения. В этих случаях ускорение точки равно нулю. Такое кинематическое состояние точки называется инерциальным, а ускорение точки равно нулю. Второй (основной) закон динамики. Произведение массы материальной точки на ускорение, которое она получает под действием силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы
На основании второго закона динамики устанавливается связь между массой тела и его весом:
где При одновременном действии на точку нескольких сил
Проектируя обе части равенства (3.3) на оси
Уравнения (3.4) являются дифференциальными уравнениями движения точки в прямоугольных декартовых координатах. Аналогично получим дифференциальные уравнения движения точки в проекциях на естественные оси:
где согласно (2.15) – (2.16) Третий закон динамики. Всякое действие вызывает равное и прямо противоположное противодействие. Отметим, что этот закон был сформулирован ранее как третья аксиома статики.
|

 тела. В классической (теоретической) механике масса тела предполагается величиной скалярной, положительной, постоянной и не зависящей от скорости тела. В основу динамики положены законы Галилея-Ньютона, являющиеся обобщением практической деятельности человека и проверяемые на опыте. Законы динамики описывают механическое движение материальных тел по отношению к неподвижным осям и по отношению к инерциальным осям. Инерциальные оси движутся относительно неподвижных осей поступательно, равномерно и прямолинейно. При движении многих задач техники оси, связанные с Землей считают неподвижными.
тела. В классической (теоретической) механике масса тела предполагается величиной скалярной, положительной, постоянной и не зависящей от скорости тела. В основу динамики положены законы Галилея-Ньютона, являющиеся обобщением практической деятельности человека и проверяемые на опыте. Законы динамики описывают механическое движение материальных тел по отношению к неподвижным осям и по отношению к инерциальным осям. Инерциальные оси движутся относительно неподвижных осей поступательно, равномерно и прямолинейно. При движении многих задач техники оси, связанные с Землей считают неподвижными. . (3.1)
. (3.1)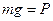 , (3.2)
, (3.2)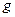 = 9,81 м/с² – ускорение свободного падения.
= 9,81 м/с² – ускорение свободного падения.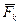 уравнение, выражающее основной закон динамики в векторной форме, с учетом равенства (2.4) принимает вид
уравнение, выражающее основной закон динамики в векторной форме, с учетом равенства (2.4) принимает вид . (3.3)
. (3.3)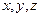 , получим:
, получим: ,
, 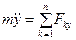 ,
, 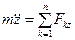 . (3.4)
. (3.4) ,
,  ,
,  , (3.5)
, (3.5) − касательное, а
− касательное, а 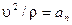 − нормальное ускорения.
− нормальное ускорения.


